题目内容
(2012•通州区一模)在直角坐标系中,点O为坐标原点,已知
=(-
,0),
=(2i-1,0)(i=1,2,…,n…),△AiBiAi+1(i=1,2,…,n…)是等边三角形,且点B1,B2,…,Bn,…在同一条抛物线C上,那么抛物线C的方程是
.
| OA1 |
| 1 |
| 4 |
| AiAi+1 |
y2=3x
y2=3x
;点B6的横坐标是| 121 |
| 4 |
| 121 |
| 4 |
分析:设Bn(x,y),先根据图形中三角形求得其坐标x,y,消去n得到x,y的关系,是一个抛物线方程,从而求得抛物线C的方程.
解答: 解:设Bn(x,y),则
解:设Bn(x,y),则
由①得x=(n-
)2,与②消去n,得y2=3x,
那么抛物线C的方程是 y2=3x;
且从①式得出点B6的横坐标是
.
故答案为:y2=3x;
.
 解:设Bn(x,y),则
解:设Bn(x,y),则
|
由①得x=(n-
| 1 |
| 2 |
那么抛物线C的方程是 y2=3x;
且从①式得出点B6的横坐标是
| 121 |
| 4 |
故答案为:y2=3x;
| 121 |
| 4 |
点评:本小题主要考查抛物线的定义、向量在几何中的应用、直线与圆锥曲线的关系等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
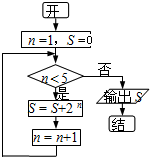 (2012•通州区一模)如图,程序框图所进行的求和运算是( )
(2012•通州区一模)如图,程序框图所进行的求和运算是( )