Question

设二次函数f（x）=ax²-4x+c（a≠0）的值域为[0，+∞），且f（1）≤4，则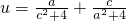的最大值是________．

Answer 1

分析：由题意可得a＞0 且△=0，求出ac=4，再由0≤f（1）≤4，得4≤a+c≤8．由函数y=t- 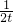在（0，+∞）上是增函数可得，对于函数u=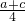-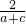，当a+c=8时，函数u有最大值为．
解答：∵二次函数f（x）=ax²-4x+c的值域为[0，+∞），
∴a＞0 且△=0，∴ac=4．
又0≤f（1）≤4，即0≤a-4+c≤4，所以4≤a+c≤8．
=====-．
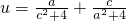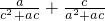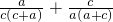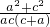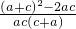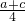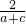由函数y=t- 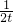在（0，+∞）上是增函数可得，对于函数u=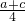-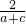，当a+c=8时，函数u有最大值为．
故答案为 ．
点评：本利用基本不等式求函数最值是高考考查的重点内容，对不符合基本不等式形式的应首先变形，然后必须满足三个条件：一正、二定、三相等．同时注意数形结合思想的运用．
是中档题．