题目内容
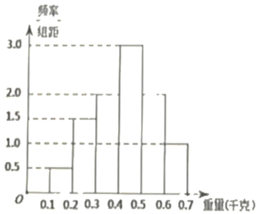
【题目】对一批产品的内径进行抽查,已知被抽查的产品的数量为200,所得内径大小统计如表所示:

(Ⅰ)以频率估计概率,若从所有的这批产品中随机抽取3个,记内径在![]() 的产品个数为X,X的分布列及数学期望
的产品个数为X,X的分布列及数学期望![]() ;
;
(Ⅱ)已知被抽查的产品是由甲、乙两类机器生产,根据如下表所示的相关统计数据,是否有![]() 的把握认为生产产品的机器种类与产品的内径大小具有相关性.
的把握认为生产产品的机器种类与产品的内径大小具有相关性.

参考公式: ,(其中
,(其中![]() 为样本容量).
为样本容量).
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
【答案】(Ⅰ)分布列见解析,![]() ;(Ⅱ)没有.
;(Ⅱ)没有.
【解析】
(Ⅰ)由频率分布表可知,任取1件产品,内径在[26,28)的概率![]() ,所以
,所以![]() ,根据二项分布的计算公式分别求出
,根据二项分布的计算公式分别求出![]() 时的概率,列出分布列,再根据期望公式求出期望;(Ⅱ)首先依题意填写
时的概率,列出分布列,再根据期望公式求出期望;(Ⅱ)首先依题意填写![]() 列联表,再求得
列联表,再求得![]() 的观测值
的观测值![]() ,结合临界值表即可得出结论。
,结合临界值表即可得出结论。
(I)任取1件产品,内径在[26,28)的概率![]() ,
,
故![]() ,
,
![]() ,
,
![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]() =
=![]() ,
,
故X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
故![]() ;
;
(II)依题意,所得列联表如下所示
内径小于28mm | 内径不小于28mm | 总计 | |
甲机器生产 | 68 | 32 | 100 |
乙机器生产 | 60 | 40 | 100 |
总计 | 128 | 72 | 200 |
![]() 的观测值为
的观测值为![]() ,
,
故没有99%的把握认为生产产品的机器种类与产品的内径大小具有相关性。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目