题目内容
17.从{1,2,3}中随机选取一个数为a,从{1,2,3,4,5}中随机选取一个数为b,则a>b的概率是( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
分析 由题意知本题是一个古典概型,试验包含的所有事件根据分步计数原理知共有3×5种结果,而满足条件的事件是a=2,b=1;a=3,b=1;a=3,b=2共有3种结果,利用古典概型公式解答.
解答 解:由题意知本题是一个古典概型,
∵试验包含的所有事件根据分步计数原理知共有3×5种结果,
而满足条件的事件是a=2,b=1;a=3,b=1;a=3,b=2共有3种结果,
∴由古典概型公式得到P=$\frac{3}{3×5}=\frac{1}{5}$;
故选:D.
点评 本题考查古典概型概率求法,关键是要找出随机事件A包含的基本事件的个数和试验中基本事件的总数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.下列选项中,说法正确的是( )
| A. | 若命题“p∨q”为真命题,则命题p和命题q均为真命题 | |
| B. | am2<bm2是a<b的必要不充分条件 | |
| C. | x=2kπ+$\frac{π}{4}$(k∈Z)是(-sinx)′=(cosx)′的充要条件 | |
| D. | 命题“若{$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{b}$+$\overrightarrow{c}$,$\overrightarrow{c}$+$\overrightarrow{a}$}构成空间的一个基底,则{$\overrightarrow{a}$,$\overrightarrow{b}$$\overrightarrow{c}$}构成空间的一个基底”的否命题为真命题 |
12.环卫工人准备在路的一侧依次栽种7棵树,现只有梧桐树和柳树可供选择,则相邻2棵树不同为柳树的栽种方法有( )
| A. | 21种 | B. | 33种 | C. | 34种 | D. | 40种 |
9.命题“对于任意的x∈R,x2+1>0”的否定是( )
| A. | 对于任意的x∈R,x2+1≤0 | B. | 存在x∈R,x2+1≤0 | ||
| C. | 存在x∈R,x2+1<0 | D. | 存在x∈R,x2+1>0 |
7.下列有关命题说法正确的是( )
| A. | 命题“若x2=4,则x=2”的否命题为“若x2=4,则x≠2” | |
| B. | 所有常数列既是等差数列也是等比数列 | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为假命题 | |
| D. | 命题“?x∈R,x2+x<0”的否定是“?x∈R,x2+x≥0”. |
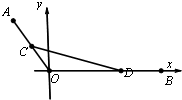 在平面直角坐标系xOy中,己知点 A(-3,4),B(9,0),C,D分别为线段OA,OB上的动点,且满足AC=BD.
在平面直角坐标系xOy中,己知点 A(-3,4),B(9,0),C,D分别为线段OA,OB上的动点,且满足AC=BD.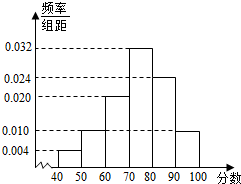 某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
某校从高一年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.