题目内容
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 作互相垂直的两条直线,与抛物线分别相交于点
作互相垂直的两条直线,与抛物线分别相交于点![]() ,
,![]() 、
、![]() 分别为弦
分别为弦![]() 、
、![]() 的中点,求
的中点,求![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() (2)16
(2)16
【解析】
(1)由抛物线定义可得![]() ,故
,故![]() ,再由点
,再由点![]() 在抛物线上代入方程即可。
在抛物线上代入方程即可。
(2)将直线![]() 的方程为
的方程为![]() 代入抛物线方程,利用韦达定理和中点坐标公式得出
代入抛物线方程,利用韦达定理和中点坐标公式得出![]() ,同理得出
,同理得出![]() 。进而求出
。进而求出![]() 和
和 ![]() ,又
,又![]() 是直角三角形易求面积,利用不等式求出面积的最小值。
是直角三角形易求面积,利用不等式求出面积的最小值。
(1)抛物线![]() 的准线方程为
的准线方程为![]() .
.
由抛物线的定义可得![]() ,故
,故![]() .
.
由点![]() 在抛物线上,可得
在抛物线上,可得![]() ,整理得
,整理得![]() ,
,
解得![]() 或
或![]() ,又
,又![]() ,所以
,所以![]() .
.
故抛物线![]() 的方程为
的方程为![]() .
.
(2)由(1)知抛物线![]() 的方程为
的方程为![]() ,焦点为
,焦点为![]() ,
,
由已知可得![]() ,所以两直线
,所以两直线![]() 的斜率都存在且均不为0.
的斜率都存在且均不为0.
设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ,
,
故直线![]() 的方程为
的方程为![]() .
.
联立方程组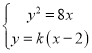 ,消去
,消去![]() ,整理得
,整理得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,
因为![]() 为弦
为弦![]() 的中点,所以
的中点,所以![]() ,
,
由![]() 得
得![]() ,故
,故![]() .
.
同理可得![]() .
.
故![]() ,
,
![]() .因为
.因为![]() ,
,
所以![]() 的面积
的面积![]()
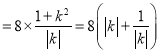
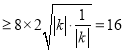 ,当且仅当
,当且仅当![]() ,即
,即![]() 时,等号成立.
时,等号成立.
所以![]() 的面积的最小值为16.
的面积的最小值为16.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案【题目】某工厂共有男女员工500人,现从中抽取100位员工对他们每月完成合格产品的件数统计如下:
每月完成合格产品的件数(单位:百件) |
|
|
|
|
|
频数 | 10 | 45 | 35 | 6 | 4 |
男员工人数 | 7 | 23 | 18 | 1 | 1 |
(1)其中每月完成合格产品的件数不少于3200件的员工被评为“生产能手”.由以上统计数据填写下面![]() 列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
非“生产能手” | “生产能手” | 合计 | |
男员工 | |||
span>女员工 | |||
合计 |
(2)为提高员工劳动的积极性,工厂实行累进计件工资制:规定每月完成合格产品的件数在定额2600件以内的,计件单价为1元;超出![]() 件的部分,累进计件单价为1.2元;超出
件的部分,累进计件单价为1.2元;超出![]() 件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.
附:![]() ,
,
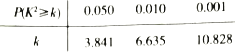 .
.
【题目】如表是我国2012年至2018年国内生产总值(单位:万亿美元)的数据:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
国内生产总值 (单位:万亿美元) | 8.5 | 9.6 | 10.4 | 11 | 11.1 | 12.1 | 13.6 |
(1)从表中数据可知![]() 和
和![]() 线性相关性较强,求出以
线性相关性较强,求出以![]() 为解释变量
为解释变量![]() 为预报变量的线性回归方程;
为预报变量的线性回归方程;
(2)已知美国2018年的国内生产总值约为20.5万亿美元,用(1)的结论,求出我国最早在那个年份才能赶上美国2018年的国内生产总值?
参考数据:![]() ,
,
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
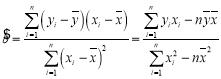 ,
,![]() .
.