题目内容
8．
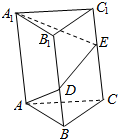一个正三棱柱底面边长为3，侧棱长为2，点D在侧棱BB1上，点E在侧棱CC1上，求AD+DE+EA1的最小值．
分析 直接利用三棱柱的侧面展开图，通过求解三角形即可得到结果．
解答 解：正三棱柱的侧面展开图如图：
由题意可知AD+DE+EA1的最小值就是侧面展开图中对角线AA1的长度，
AA1=$\sqrt{{2}^{2}+{9}^{2}}$=$\sqrt{85}$．
点评 本题考查几何体表面距离的最值问题，考查空间想象能力以及计算能力．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
20．把直线x-y+1=0沿向量$\overrightarrow{a}$=（1，0）方向平移，使之与圆（x-2）2+（y-1）2=1相切，则平移的距离为（ ）
| A． | $\sqrt{2}-1$ | B． | $\sqrt{2}+2$ | C． | $\sqrt{2}-1$与$\sqrt{2}+1$ | D． | 2-$\sqrt{2}$与2+$\sqrt{2}$ |
18．已知a＞0，“x∈{-a，a}”是“|x|=a”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 非充分非必要条件 |