题目内容
19.求函数f(x)=x2-2ax+3在区间[1,3]上的最大值和最小值.分析 求f(x)的对称轴为x=a,讨论a和区间[1,3]的关系:分a≤1,1<a<3,a≥3,这三种情况,对于每种情况根据二次函数f(x)在[1,3]上的单调性,或取到顶点值,或比较端点值,这样即可得出每种情况下的函数f(x)的最大值和最小值.
解答 解:f(x)的对称轴为x=a;
(1)若a≤1,则f(x)在[1,3]上单调递增;
∴f(x)的最大值为f(3)=12-6a,最小值为f(1)=4-2a;
(2)若1<a<3,则f(a)=-a2+3是f(x)的最小值;
f(1)-f(3)=4a-8;
∴①1<a≤2时,f(3)=12-6a为f(x)的最大值;
②2<x<3时,f(1)=4-2a为f(x)的最大值;
(3)若a≥3,则f(x)在[1,3]上单调递减;
∴f(x)的最大值为f(1)=4-2a,最小值为f(3)=12-6a.
点评 考查二次函数的对称轴的求解公式,二次函数的单调性,以及根据单调性求函数的最大值、最小值,根据取得顶点的情况或比较端点值来求二次函数最值的方法,要熟悉二次函数的图象.

练习册系列答案
相关题目
14.执行如图所示的程序框图,若输入x=4,则输出y的值为( )
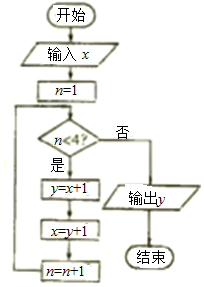

| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
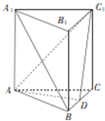 如图,在三棱柱ABC-A1B1C1中,底面ABC为正三角形,CC1⊥平面ABC,AB=AA1,D是BC上的一点,且AD⊥C1D.
如图,在三棱柱ABC-A1B1C1中,底面ABC为正三角形,CC1⊥平面ABC,AB=AA1,D是BC上的一点,且AD⊥C1D.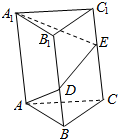 一个正三棱柱底面边长为3,侧棱长为2,点D在侧棱BB1上,点E在侧棱CC1上,求AD+DE+EA1的最小值.
一个正三棱柱底面边长为3,侧棱长为2,点D在侧棱BB1上,点E在侧棱CC1上,求AD+DE+EA1的最小值.