题目内容
(1)求函数 的单调区间;
的单调区间;
(2)比较tan 1、tan 2、tan 3的大小.
答案:略
解析:
提示:
解析:
|
解: (1)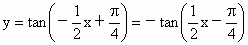 ,则由 ,则由
∴函数  的单调递减区间是 的单调递减区间是 (kÎ
Z). (kÎ
Z).
(2)∵tan 2=tan(2-p ),tan 3=tan(3-p ), 又∵ ∵ 且 y=tan x在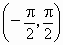 内是增函数, 内是增函数,
∴ tan(2-p )<tan(3-p )<tan 1,即tan2<tan3<tan1. 对于(1),由于x的系数小于零,故应将其进行变形,化为系数为正,再根据正切函数单调性求解;对于(2)可利用正切函数单调性进行比较. |
提示:
|
(1)求y=Atan(ωx+j )的单调区间,只需要令
(2)比较两个同名函数值的大小,应转化到同一单调区间上来比较.对不同名的三角函数,应先化为同名的. |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
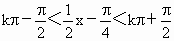 得
得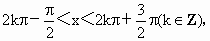
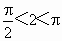 ,∴
,∴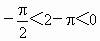 .
.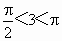 ,∴
,∴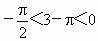 ,显然
,显然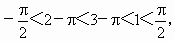
 解出x即可,但ω<0时,应用诱导公式化为正的,还要注意A的正负对单调性的影响.
解出x即可,但ω<0时,应用诱导公式化为正的,还要注意A的正负对单调性的影响.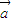 ,
, ,
,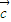 ,
, 及实数x,y且|
及实数x,y且|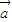 |=|
|=| |=1,
|=1, =
= +(x2-3)x
+(x2-3)x ,
,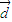 =-y
=-y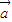 +
+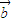 ,
,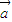 ⊥
⊥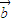 ,
, ⊥
⊥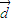 .
.