题目内容
已知向量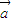 ,
, ,
,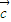 ,
, 及实数x,y且|
及实数x,y且|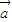 |=|
|=| |=1,
|=1, =
= +(x2-3)x
+(x2-3)x ,
,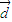 =-y
=-y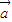 +
+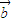 ,
,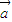 ⊥
⊥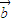 ,
, ⊥
⊥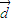 .
.(1)求y关于x的函数关系式y=f(x);
(2)求函数y=f(x)的单调区.
【答案】分析:(1)利用向量数量积公式,化简可得函数解析式;
(2)求导函数,利用导数的正负,可得函数的单调区间.
解答:解:(1)∵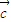 =
=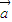 +(x2-3)x
+(x2-3)x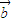 ,
,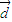 =-y
=-y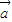 +
+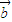 ,
,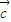 ⊥
⊥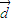 ,
,
∴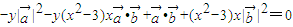
∵|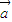 |=|
|=|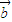 |=1,
|=1,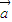 ⊥
⊥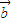 ,
,
∴y=x3-3x,即f(x)=x3-3x;
(2)求导数可得y′=3x2-3=3(x+1)(x-1)
令y′>0,可得x<-1或x>1;令y′<0,可得-1<x<1,
∴函数的得到递增区间是(-∞,-1),(1,+∞),单调递减区间是(-1,1).
点评:本题考查向量知识的运用,考查导数知识,考查函数的单调性,确定函数解析式是关键.
(2)求导函数,利用导数的正负,可得函数的单调区间.
解答:解:(1)∵
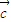 =
=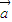 +(x2-3)x
+(x2-3)x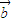 ,
,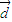 =-y
=-y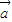 +
+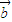 ,
,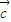 ⊥
⊥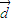 ,
,∴
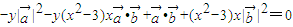
∵|
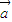 |=|
|=|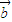 |=1,
|=1,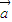 ⊥
⊥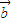 ,
,∴y=x3-3x,即f(x)=x3-3x;
(2)求导数可得y′=3x2-3=3(x+1)(x-1)
令y′>0,可得x<-1或x>1;令y′<0,可得-1<x<1,
∴函数的得到递增区间是(-∞,-1),(1,+∞),单调递减区间是(-1,1).
点评:本题考查向量知识的运用,考查导数知识,考查函数的单调性,确定函数解析式是关键.

练习册系列答案
相关题目
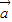 、
、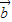 、
、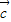 、
、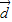 及实数x、y满足
及实数x、y满足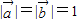 ,
,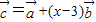 ,
, ,若
,若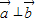 ,
,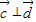 且
且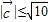 .
.