Question

已知函数f（x）=lnx，g（x）=

1

2

x2+mx+

7

2

（m＜0），直线l与函数f（x），g（x）的图象都相切，且与函数f（x）的图象的切点横坐标为1．
（1）求直线l的方程及m的值；
（2）若h（x）=f（x）-g'（x）（其中g'（x）是g（x）的导函数），求h（x）的单调区是及最值．

Answer 1

分析：（1）欲求出切线方程，只须求出其斜率即可，故先利用导数求出在x=1处的导函数值，再结合导数的几何意义即可求出切线的斜率，最后利用直线方程与曲线方程组成的方程有唯一解求得m．从而问题解决．
（2）令h'（x）=0求出x的值为x=1，分两种情况讨论h'（x）的正负得到函数的单调区间，根据函数的增减性即可得到函数的最小值．

解答：解：（1）由题意可知直线l与函数f（x）=lnx相切于（1，0）．∵f′(x)=

1

x

∴切线斜率k=f'（1）=1∴切线l的方程为y=x-1
又∵直线l与g(x)=

1

2

x2+mx+

7

2

(m＜0)相切．
即方程

1

2

x2+mx+

7

2

=x-1有一个解．∴△=(m-1)2-4•

1

2

•

9

2

=0(m＜0)∴m=-2
（2）由（1）可知g(x)=

1

2

x2-2x+

7

2

∴g'（x）=x-2，∴h(x)=lnx-x+2(x＞0)∴h′(x)=

1

x

-1
由h'（x）=0，得x=1，h'（x）及h（x）的变化如下表

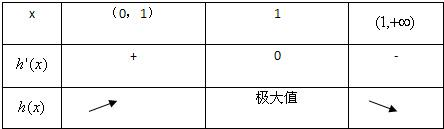
故h（x）的单调增区间为（0，1），单调减区间为（1，+∞），h（x）_max=h（1）=1，无最小值．

点评：考查学生会利用导数求曲线上过某点切线方程的斜率，会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值．灵活运用分类讨论的数学思想解决数学问题．