题目内容
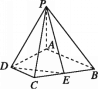
【题目】如图,在四棱锥P﹣ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点. 
(1)求证:PC∥平面BMN;
(2)求证:平面BMN⊥平面PAC. 
【答案】
(1)证明:设AC∩BN=O,连结MO,AN,
因为 ![]() ,N为CD的中点,
,N为CD的中点,
所以AB=CN,AB∥CN,所以四边形ABCN为平行四边形,
所以O为AC的中点,所以MO∥PC.
又因为MO平面BMN,PC平面BMN,所以PC∥平面BMN
(2)证明:(方法一)因为PC⊥平面PDA,AD平面PDA
所以PC⊥AD,由(1)同理可得,四边形ABND为平行四边形,
所以AD∥BN,所以BN⊥PC
因为BC=AB,所以平行四边形ABCN为菱形,所以BN⊥AC,
因为PC∩AC=C,AC平面PAC,PC平面PAC,所以BN⊥平面PAC
因为BN平面BMN,所以平面BMN⊥平面PAC.
(方法二)连结PN,因为PC⊥平面PDA,PA平面PDA,所以PC⊥PA
因为PC∥MO,所以PA⊥MO,因为PC⊥平面PDA,PD平面PDA,所以PC⊥PD
因为N为CD的中点,所以 ![]() ,由(1)
,由(1) ![]() ,所以AN=PN
,所以AN=PN
又因为M为PA的中点,所以PA⊥MN
因为MN∩MO=M,MN平面BMN,MO平面BMN
所以PA⊥平面BMN,因为PA平面PAC,所以平面PAC⊥平面BMN.
【解析】
【考点精析】掌握直线与平面平行的判定和平面与平面垂直的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直.

【题目】冶炼某种金属可以用旧设备和改造后的新设备,为了检验用这两种设备生产的产品中所含杂质的关系,调查结果如下表所示:
分类 | 杂质高 | 杂质低 |
旧设备 | 37 | 121 |
新设备 | 22 | 202 |
根据以上数据,则( )
A. 含杂质的高低与设备改造有关
B. 含杂质的高低与设备改造无关
C. 设备是否改造决定含杂质的高低
D. 以上答案都不对
【题目】已知M,N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,线段MN的中点A的横坐标为![]() .
.
(1)求|MF|+|NF|的值;
(2)若p=2,直线MN与x轴交于点B,求点B的横坐标的取值范围.
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进
,并根据以下不等式进
行评判(![]() 表示相应事件的概率);①
表示相应事件的概率);①![]() ;②
;②![]() ;③
;③![]() .
.
评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备![]() 的性能等级.
的性能等级.
(2)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品.
的零件认为是次品.
(ⅰ)从设备![]() 的生产流水线上随意抽取2件零件,计算其中次品个数
的生产流水线上随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() ;
;
(ⅱ)从样本中随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() .
.