Question

【题目】已知非空集合M满足M{0，1，2，…，n}（n≥2，n∈N+）．若存在非负整数k（k≤n），使得当a∈M时，均有2k﹣a∈M，则称集合M具有性质P．设具有性质P的集合M的个数为f（n）．
（1）求f（2）的值；
（2）求f（n）的表达式．

Answer 1

【答案】
（1）解：当n=2时，M={0}，{1}，{2}，{0，2}，{0，1，2}具有性质P，

对应的k分别为0，1，2，1，1，故f（2）=5．

（2）解：可知当n=k时，具有性质P的集合M的个数为f（t），

则当n=k+1时，f（t+1）=f（t）+g（t+1），

其中g（t+1）表达t+1∈M也具有性质P的集合M的个数，

下面计算g（t+1）关于t的表达式，

此时应有2k≥t+1，即 ，故对n=t分奇偶讨论，

①当t为偶数时，t+1为奇数，故应该有 ，

则对每一个k，t+1和2k﹣t﹣1必然属于集合M，且t和2k﹣t，…，k和k共有t+1﹣k组数，每一组数中的两个数必然同时属于或不属于集合M，

故对每一个k，对应的具有性质P的集合M的个数为 ，

所以 ，

②当t为奇数时，t+1为偶数，故应该有 ，

同理 ，

综上，可得 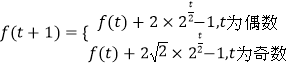又f（2）=5，

由累加法解得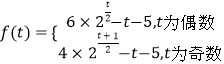

即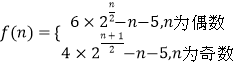

【解析】（1）当n=2时，M={0}，{1}，{2}，{0，2}，{0，1，2}具有性质P，求出对应的k，即可得出．（2）可知当n=k时，具有性质P的集合M的个数为f（t），当n=k+1时，f（t+1）=f（t）+g（t+1），其中g（t+1）表达t+1∈M也具有性质P的集合M的个数，
计算g（t+1）关于t的表达式，此时应有2k≥t+1，即 ，故对n=t分奇偶讨论，利用集合M具有性质P即可得出．
【考点精析】解答此题的关键在于理解集合的表示方法-特定字母法的相关知识，掌握①自然语言法：用文字叙述的形式来描述集合.②列举法：把集合中的元素一一列举出来，写在大括号内表示集合.③描述法：{|具有的性质}，其中为集合的代表元素.④图示法：用数轴或韦恩图来表示集合．