题目内容
【题目】为评估设备
生产某种零件的性能，从设备生产零件的流水线上随机抽取100件零件作为样本，测量其直径后，整理得到下表：
直径mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算，样本的平均值
，标准差
，以频率值作为概率的估计值.
（1）为评判一台设备的性能，从该设备加工的零件中任意抽取一件，记其直径为
，并根据以下不等式进
行评判（
表示相应事件的概率）；①
；②
；③
.
评判规则为：若同时满足上述三个不等式，则设备等级为甲；仅满足其中两个，则等级为乙；若仅满足其中一个，则等级为丙；若全部不满足，则等级为丁，试判断设备的性能等级.
（2）将直径小于等于
或直径大于
的零件认为是次品.
（ⅰ）从设备的生产流水线上随意抽取2件零件，计算其中次品个数
的数学期望
；
（ⅱ）从样本中随意抽取2件零件，计算其中次品个数
的数学期望
.
【答案】(1)见解析（2）见解析
【解析】
（1）根据3
原则，分别求得其对应的概率，进而判断出M的性能级别。
（2）通过题意可知，样本中共有6件次品，可知M生产的次品率为0.06。通过二项分布的概率分布即可求得次品的数学期望。
（1）由题意知道：
，
，
，
，
，
，所以由图表知道：
所以该设备
的性能为丙级别.
（2）由图表知道：直径小于或等于
的零件有2件，大于
的零件有4件，共计6件
（i）从设备的生产流水线上任取一件，取到次品的概率为
，
依题意
，
故
（ii）从100件样品中任意抽取2件，次品数
的可能取值为0，1，2
，
，
，
故
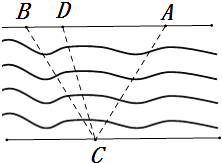
【题目】如图，在等腰梯形ABCD中，AB=2，CD=4，BC= 
，点E，F分别为AD，BC的中点．如果对于常数λ，在ABCD的四条边上，有且只有8个不同的点P使得 
=λ成立，那么实数λ的取值范围为 ． 
【题目】某研究机构对某校高二文科学生的记忆力x和判断力y进行统计分析，得下表数据．
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图；
(2)请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；
(3)试根据(2)中求出的线性回归方程，预测记忆力为14的学生的判断力．
【题目】高中生在被问及“家，朋友聚集的地方，个人空间”三个场所中“感到最幸福的场所在哪里？”这个问题时，从中国某城市的高中生中，随机抽取了55人，从美国某城市的高中生中随机抽取了45人进行答题.中国高中生答题情况是：选择家的占
、朋友聚集的地方占
、个人空间占.美国高中生答题情况是：朋友聚集的地方占
、家占
、个人空间占.如下表：
在家里最幸福 | 在其它场所幸福 | 合计 | |
中国高中生 | |||
美国高中生 | |||
合计 |
（Ⅰ）请将
列联表补充完整；试判断能否有
的把握认为“恋家”与否与国别有关；
（Ⅱ）从被调查的不“恋家”的美国学生中，用分层抽样的方法选出4人接受进一步调查，再从4人中随机抽取2人到中国交流学习，求2人中含有在“个人空间”感到幸福的学生的概率.
附：
，其中
.
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.828 |
