题目内容
14．在△ABC中，角A，B，C所对边长分别为a，b，c，若（b-c）2-a2=-bc，则sinA=$\frac{\sqrt{3}}{2}$．分析 由已知整理可得：b2+c2-a2=bc，利用余弦定理可得cosA=$\frac{1}{2}$，结合0＜A＜π可解得sinA的值．
解答 解：∵（b-c）2-a2=-bc，
∴整理可得：b2+c2-a2=bc，
∴由余弦定理可得：cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{bc}{2bc}$=$\frac{1}{2}$，
∴结合0＜A＜π可得：sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{\sqrt{3}}{2}$．
故答案为：$\frac{\sqrt{3}}{2}$．
点评 本题主要考查了余弦定理，同角三角函数关系式的应用，属于基础题．
练习册系列答案
计算高手系列答案
相关题目
6．已知数列{an}满足a1=0，an+1=$\frac{{{a_n}-2}}{{\frac{5}{4}{a_n}-2}}$，则a2015=（ ）
| A． | 0 | B． | 1 | C． | $\frac{4}{3}$ | D． | 2 |
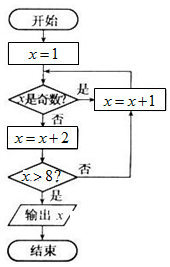
在第十六届广州亚运会上，某项目的比赛规则为：由两人（记为甲和乙）进行比赛，每局胜者得1分，负者得0分（无平局），比赛进行到有一人比对方多2分或打满6局时停止．设甲在每局中获胜的概率为p（p＞0.5），且各局胜负相互独立．已知第二局比赛结束时比赛停止的概率为$\frac{5}{9}$．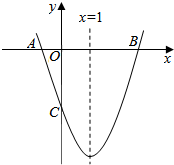
如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为x=1，且抛物线经过A（-1，0）、C（0，-3）两点，与x轴交于另一点B．
的零点所在区间是（ ）
B．
C．
D．
，若当
时，不等式
恒成立，则实数
的取值范围是（ ）
B．
D．
如图，割线PBC经过圆心O，PB=OB=1，OB绕点O逆时针旋$\frac{2π}{3}$到OD，连PD交圆O于点E，则PE=$\frac{3\sqrt{7}}{7}$．