题目内容
19.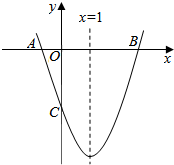 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.(1)求这条抛物线所对应的函数关系式;
(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标;
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.
分析 (1)设出二次函数的表达式,列出方程组,考查即可求出抛物线的解析式;
(2)先求出抛物线和x轴交点的坐标,求出直线的解析式,从而求出M点的坐标;
(3)法一:先求出直线BC的解析式,进而求出PC的解析式,从而求出P点的坐标,法二:根据勾股定理求出即可.
解答 解:(1)设抛物线的解析式为y=ax2+bx+c,
则有:$\left\{\begin{array}{l}a-b+c=0\\ c=-3\\-\frac{b}{2a}=1\end{array}\right.$解得:$\left\{\begin{array}{l}a=1\\ b=-2\\ c=-3\end{array}\right.$,
所以抛物线的解析式为y=x2-2x-3.
(2)令x2-2x-3=0,解得x1=-1,x2=3,
所以B点坐标为(3,0),
设直线BC的解析式为y=kx+b,
则$\left\{\begin{array}{l}3k+b=0\\ b=-3\end{array}\right.$,解得$\left\{\begin{array}{l}k=1\\ b=-3\end{array}\right.$,
所以直线解析式是y=x-3;
当x=1时,y=-2,所以M点的坐标为(1,-2).
(3)方法一:要使∠PBC=90°,
则直线PC过点C,且与BC垂直,
又直线BC的解析式为y=x-3,
所以直线PC的解析式为y=-x-3,当x=1时,y=-4,
所以P点坐标为(1,-4).
方法二:设P点坐标为(1,y),
则PC2=12+(-3-y)2,BC2=32+32;PB2=22+y2
由∠PBC=90°可知△PBC是直角三角形,且PB为斜边,
则有PC2+BC2=PB2.
所以:[12+(-3-y)2]+[32+32]=22+y2;解得y=-4,
所以P点坐标为(1,-4).
点评 本题考查了二次函数的性质的综合应用,考查求函数的解析式问题,是一道中档题.

| A. | (-∞,1) | B. | (-∞,-1) | C. | (-1,+∞) | D. | (1,+∞) |
| A. | A${\;}_{100}^{10}$ | B. | A${\;}_{100}^{11}$ | C. | A${\;}_{100}^{12}$ | D. | A${\;}_{101}^{11}$ |
 ,使
,使 的否定为:
的否定为: ,均有
,均有 ,则
,则 的逆命题为:若
的逆命题为:若 或
或 ,则
,则
 ,则幂函数
,则幂函数 为偶函数,且在
为偶函数,且在 上单调递减的充要条件为
上单调递减的充要条件为
 的图像关于点
的图像关于点 中心对称的充分必要条件为
中心对称的充分必要条件为
 中,
中, 所对的边为
所对的边为 ,
, ,且
,且 .
. 的大小;
的大小; ,求
,求 与
与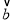 的夹角等于
的夹角等于 ,如果
,如果 ,那么
,那么 ( )
( ) B.9 C.
B.9 C. D.10
D.10