题目内容
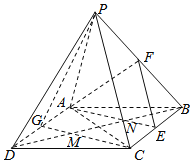
【题目】如图,四边形ABCD是平行四边形,点E,F,G分别为线段BC,PB,AD的中点.

(1)证明:EF∥平面PAC;
(2)证明:平面PCG∥平面AEF;
(3)在线段BD上找一点H,使得FH∥平面PCG,并说明理由.
【答案】(1)见解析 (2)见解析 (3)见解析
【解析】
(1)证明![]() ,EF∥平面PAC即得证;(2)证明AE∥平面PCG,EF∥平面PCG,平面PCG∥平面AEF即得证;(3)设AE,GC与BD分别交于M,N两点,证明N点为所找的H点.
,EF∥平面PAC即得证;(2)证明AE∥平面PCG,EF∥平面PCG,平面PCG∥平面AEF即得证;(3)设AE,GC与BD分别交于M,N两点,证明N点为所找的H点.
(1)证明:∵E、F分别是BC,BP中点,
∴![]() ,
,
∵PC平面PAC,EF平面PAC,
∴EF∥平面PAC.
(2)证明:∵E、G分别是BC、AD中点,
∴AE∥CG,
∵AE平面PCG,CG平面PCG,
∴AE∥平面PCG,
又∵EF∥PC,PC平面PCG,EF平面PCG,
∴EF∥平面PCG,AE∩EF=E点,AE,EF平面AEF,
∴平面AEF∥平面PCG.
(3)设AE,GC与BD分别交于M,N两点,易知F,N分别是BP,BM中点,
∴![]() ,
,
∵PM平面PGC,FN平面PGC,
∴FN∥平面PGC,
即N点为所找的H点.

【题目】某工厂每日生产一种产品![]() 吨,每日生产的产品当日销售完毕,日销售额为
吨,每日生产的产品当日销售完毕,日销售额为![]() 万元,产品价格随着产量变化而有所变化,经过段时间的产销, 得到了
万元,产品价格随着产量变化而有所变化,经过段时间的产销, 得到了![]() 的一组统计数据如下表:
的一组统计数据如下表:
日产量 | 1 | 2 | 3 | 4 | 5 |
日销售量 | 5 | 12 | 16 | 19 | 21 |
(1)请判断![]() 与
与![]() 中,哪个模型更适合到画
中,哪个模型更适合到画![]() 之间的关系?可从函数增长趋势方面给出简单的理由;
之间的关系?可从函数增长趋势方面给出简单的理由;
(2)根据你的判断及下面的数据和公式,求出![]() 关于
关于![]() 的回归方程,并估计当日产量
的回归方程,并估计当日产量![]() 时,日销售额是多少?
时,日销售额是多少?
参考数据:![]() ,
,![]()
![]()
线性回归方程![]() 中,
中, ,
,![]() ,
,
【题目】随着西部大开发的深入,西南地区的大学越来越受到广大考生的青睐.下表是西南地区某大学近五年的录取平均分与省一本线对比表:
年份 |
|
|
|
|
|
年份代码 |
|
|
|
|
|
省一本线 |
|
|
|
|
|
录取平均分 |
|
|
|
|
|
录取平均分与省一本线分差 |
|
|
|
|
|
(1)根据上表数据可知,![]() 与
与![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的性回归方程;
的性回归方程;
(2)假设2019年该省一本线为![]() 分,利用(1)中求出的回归方程预测2019年该大学录取平均分.
分,利用(1)中求出的回归方程预测2019年该大学录取平均分.
参考公式: ,
,![]()
【题目】某煤炭公司销售人员根据该公司以往的销售情况,得到如下频率分布表
日销售量分组 | [2,4) | [4,6) | [6,8) | [8,10) | [10,12] |
频率 | 0.10 | 0.20 | 0.30 | 0.25 | 0.15 |
(1)在下图中作出这些数据的频率分布直方图;

(2)将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.若未来3天内日销售量不低于6吨的天数为X,求X的分布列、数学期望与方差.
