Question

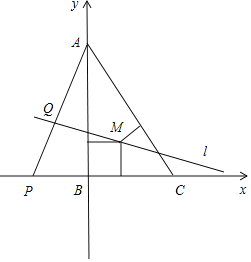
【题目】在Rt△ABC中，∠B＝90°，BC＝6，AB＝8，点M为△ABC内切圆的圆心，过点M作动直线l与线段AB，AC都相交，将△ABC沿动直线l翻折，使翻折后的点A在平面BCM上的射影P落在直线BC上，点A在直线l上的射影为Q，则的最小值为_____．

Answer 1

【答案】825

【解析】

以AB，BC所在直线为坐标轴建立平面直角坐标系，设直线l的斜率为k，用k表示出|PQ|，|AQ|，利用基本不等式得出答案．

过点M作△ABC的三边的垂线，设⊙M的半径为r，则r2，

以AB，BC所在直线为坐标轴建立平面直角坐标系，

如图所示，则M（2，2），A（0，8），

因为A在平面BCM的射影在直线BC上，所以直线l必存在斜率，

过A作AQ⊥l，垂足为Q，交直线BC于P，

设直线l的方程为：y＝k（x﹣2）+2，则|AQ|，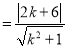

又直线AQ的方程为：yx+8，则P（8k，0），所以|AP|8，

所以|PQ|＝|AP|﹣|AQ|＝8，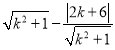

所以，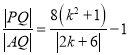

①当k＞﹣3时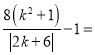，4（k+3）25≥825，

当且仅当4（k+3），即k3时取等号；

②当k＜﹣3时，则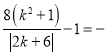4（k+3）23≥823，

当且仅当﹣4（k+3），即k3时取等号.

故答案为：825