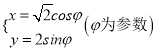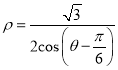题目内容
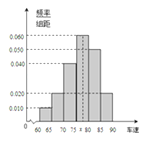
【题目】2012年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:(60,65),[65,70),[70,75),[80,85),[85,90)后得到如图的频率分布直方图.
(1)某调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的众数和中位数的估计值.
(3)若从车速在[60,70)的车辆中任抽取2辆,求车速在[65,70)的车辆至少有一辆的概率.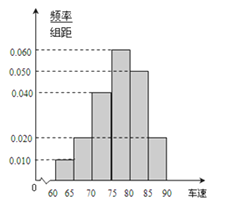
【答案】解:(1)由题意知这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,是一个具有相同间隔的抽样,并且总体的个数比较多,这是一个系统抽样.
故调查公司在采样中,用到的是系统抽样,
(2)众数的估计值为最高的矩形的中点,即众数的估计值等于77.5
设图中虚线所对应的车速为x,则中位数的估计值为:
0.01×5+0.02×5+0.04×5+0.06×(x﹣75)=0.5,
解得x=77.5,即中位数的估计值为77.5
(3)从图中可知,车速在[60,65)的车辆数为:m1=0.01×5×40=2(辆),
车速在[65,70)的车辆数为:m2=0.02×5×40=4(辆)
设车速在[60,65)的车辆设为a,b,车速在[65,70)的车辆设为c,d,e,f,
则所有基本事件有:(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)共15种 (10分)
其中车速在[65,70)的车辆至少有一辆的事件有:(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f)共14种
所以,车速在[65,70)的车辆至少有一辆的概率为P=![]() .
.
【解析】(1)这个抽样是按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,是一个具有相同间隔的抽样,并且总体的个数比较多,这是一个系统抽样;
(2)选出直方图中最高的矩形求出其底边的中点即为众数;求出从左边开始小矩形的面积和为0.5对应的横轴的左边即为中位数;利用各个小矩形的面积乘以对应矩形的底边的中点的和为数据的平均数.
(3)从图中可知,车速在[60,65)的车辆数和车速在[65,70)的车辆数.从车速在(60,70)的车辆中任抽取2辆,设车速在[60,65)的车辆设为a,b,车速在[65,70)的车辆设为c,d,e,f,列出各自的基本事件数,从而求出相应的概率即可.
【考点精析】根据题目的已知条件,利用用样本的频率分布估计总体分布的相关知识可以得到问题的答案,需要掌握样本数据的频率分布表和频率分布直方图,是通过各小组数据在样本容量中所占比例大小来表示数据的分布规律,它可以让我们更清楚的看到整个样本数据的频率分布情况,并由此估计总体的分布情况.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】在一次模拟考试后,从高三某班随机抽取了20位学生的数学成绩,其分布如下:
分组 | [90,100] | [100,110) | [110,120) | [120,130) | [130,140) | [140,150) |
频数 | 1 | 2 | 6 | 7 | 3 | 1 |
分数在130分(包括130分)以上者为优秀,据此估计该班的优秀率约为( )
A.10%
B.20%
C.30%
D.40%