题目内容
在平面直角坐标系中,给定 ,点
,点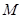 为
为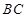 的中点,点
的中点,点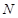 满足
满足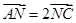 ,点
,点 满足
满足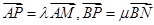 .
.
(1)求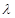 与
与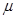 的值;
的值;
(2)若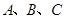 三点坐标分别为
三点坐标分别为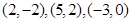 ,求
,求 点坐标.
点坐标.
(1) ;(2)
;(2) 点的坐标为
点的坐标为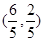 .
.
解析试题分析:先引入平面向量的基底,如 ,然后将
,然后将 分别用基底表示,最后得到
分别用基底表示,最后得到 ,而另一方面
,而另一方面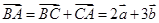 ,再根据平面向量的基本定理得到方程组
,再根据平面向量的基本定理得到方程组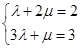 ,求解方程组即可;(2)先确定
,求解方程组即可;(2)先确定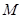 的坐标,设
的坐标,设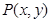 ,再结合
,再结合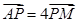 ,得到
,得到 ,从而得到
,从而得到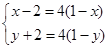 ,求解即可得到
,求解即可得到 点的坐标.
点的坐标.
试题解析:(1)设
则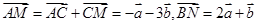 2分
2分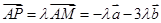 ,
,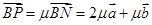 ,
,
故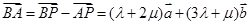 4分
4分
而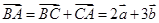
由平面向量基本定理得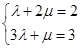 ,解得
,解得 6分
6分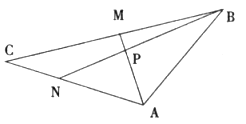
(2)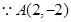 、
、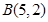 、
、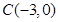 ,由于
,由于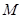 为
为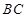 中点,
中点,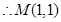 9分
9分
设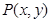 ,又由(1)知
,又由(1)知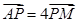
所以
可得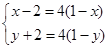 ,解之得
,解之得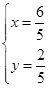
所以 点的坐标为
点的坐标为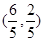 12分.
12分.
考点:1.平面向量的线性运算;2.平面向量的基本定理;3.平面向量的坐标运算.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
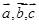 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 .
. ,且
,且 ,求向量
,求向量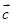 ;
; ,且
,且 与
与 垂直,求
垂直,求 与
与 的夹角的正弦值.
的夹角的正弦值.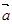 、
、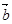 是不共线的两个非零向量.
是不共线的两个非零向量. ,求证:
,求证: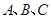 三点共线;
三点共线;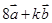 与
与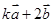 共线,求实数
共线,求实数 的值.
的值. ,点
,点 为直线
为直线 上的一个动点.
上的一个动点. 恒为锐角;
恒为锐角; 为菱形,求
为菱形,求 的值.
的值.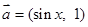 ,
,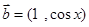 ,函数
,函数 ,
,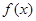 的值域;
的值域; ,且
,且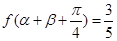 ,
, ,求
,求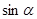 的值。
的值。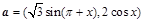 ,
,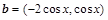 ,已知函数
,已知函数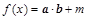 在
在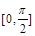 上的最大值为6.
上的最大值为6. 的值;
的值;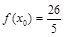 ,
,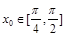 .求
.求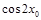 的值.
的值.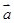 =(1,2),
=(1,2),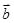 =(2,-2).
=(2,-2).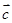 =4
=4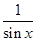 ,
,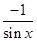 ),b=(2,cos2x).
),b=(2,cos2x).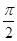 ],试判断a与b能否平行?
],试判断a与b能否平行?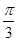 ],求函数f(x)=a·b的最小值.
],求函数f(x)=a·b的最小值.  =(2,4),
=(2,4), =(1,3),则
=(1,3),则 的坐标是 .
的坐标是 .