题目内容
（2013•上海）已知正方形ABCD的边长为1，记以A为起点，其余顶点为终点的向量分别为
，
，
；以C为起点，其余顶点为终点的向量分别为
，
，
，若i，j，k，l∈{1，2，3}，且i≠j，k≠l，则(
+
)•(
+
)的最小值是
| a1 |
| a2 |
| a3 |
| c1 |
| c2 |
| c3 |
| ai |
| aj |
| ck |
| cl |
-5
-5
．分析：如图建立直角坐标系．不妨记以A为起点，其余顶点为终点的向量
，
，
分别为
，
，
，以C为起点，其余顶点为终点的向量
，
，
分别为
，
，
．再分类讨论当i，j，k，l取不同的值时，利用向量的坐标运算计算(
+
)•(
+
)的值，从而得出(
+
)•(
+
)的最小值．
| a1 |
| a2 |
| a3 |
| AB |
| AC |
| AD |
| c1 |
| c2 |
| c3 |
| CD |
| CA |
| CB |
| ai |
| aj |
| ck |
| cl |
| ai |
| aj |
| ck |
| cl |
解答：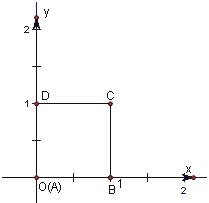
解：不妨记以A为起点，其余顶点为终点的向量
，
，
分别为
，
，
，以C为起点，其余顶点为终点的向量
，
，
分别为
，
，
．如图建立坐标系．
（1）当i=1，j=2，k=1，l=2时，则(
+
)•(
+
)=[（1，0）+（1，1）]•[（（-1，0）+（-1，-1）]=-5；
（2）当i=1，j=2，k=1，l=3时，则(
+
)•(
+
)=[（1，0）+（1，1）]•[（（-1，0）+（0，-1）]=-3；
（3）当i=1，j=2，k=2，l=3时，则(
+
)•(
+
)=[（1，0）+（1，1）]•[（（-1，-1）+（0，-1）]=-4；
（4）当i=1，j=3，k=1，l=2时，则(
+
)•(
+
)=[（1，0）+（0，1）]•[（（-1，0）+（-1，-1）]=-3；
同样地，当i，j，k，l取其它值时，(
+
)•(
+
)=-5，-4，或-3．
则(
+
)•(
+
)的最小值是-5．
故答案为：-5．
解：不妨记以A为起点，其余顶点为终点的向量| a1 |
| a2 |
| a3 |
| AB |
| AC |
| AD |
| c1 |
| c2 |
| c3 |
| CD |
| CA |
| CB |
（1）当i=1，j=2，k=1，l=2时，则(
| ai |
| aj |
| ck |
| cl |
（2）当i=1，j=2，k=1，l=3时，则(
| ai |
| aj |
| ck |
| cl |
（3）当i=1，j=2，k=2，l=3时，则(
| ai |
| aj |
| ck |
| cl |
（4）当i=1，j=3，k=1，l=2时，则(
| ai |
| aj |
| ck |
| cl |
同样地，当i，j，k，l取其它值时，(
| ai |
| aj |
| ck |
| cl |
则(
| ai |
| aj |
| ck |
| cl |
故答案为：-5．
点评：本小题主要考查平面向量坐标表示、平面向量数量积的运算等基本知识，考查考查分类讨论、化归以及数形结合等数学思想方法，考查分析问题、解决问题的能力．
练习册系列答案
相关题目
（2013•上海）已知圆柱Ω的母线长为l，底面半径为r，O是上底面圆心，A，B是下底面圆周上两个不同的点，BC是母线，如图，若直线OA与BC所成角的大小为