题目内容
（2013•上海）已知圆柱Ω的母线长为l，底面半径为r，O是上底面圆心，A，B是下底面圆周上两个不同的点，BC是母线，如图，若直线OA与BC所成角的大小为| π |
| 6 |
| l |
| r |
| 3 |
| 3 |
分析：过A作与BC平行的母线AD，由异面直线所成角的概念得到∠OAD为
．在直角三角形ODA中，直接由cot
=
得到答案．
| π |
| 6 |
| π |
| 6 |
| l |
| r |
解答：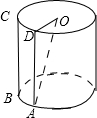
解：如图，过A作与BC平行的母线AD，连接OD，则∠OAD为直线OA与BC所成的角，大小为
．
在直角三角形ODA中，因为∠OAD=
，所以cot
=
．
则
=
．
故答案为
解：如图，过A作与BC平行的母线AD，连接OD，则∠OAD为直线OA与BC所成的角，大小为| π |
| 6 |
在直角三角形ODA中，因为∠OAD=
| π |
| 6 |
| π |
| 6 |
| l |
| r |
则
| l |
| r |
| 3 |
故答案为
| 3 |
点评：本题考查了异面直线所成的角，考查了直角三角形的解法，是基础题．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目