题目内容
20．作出下列函数的图象．（1）y=|x2-2x|+1；
（2）y=$\frac{2-x}{x-3}$．
分析 （1）y=|x2-2x|+1=$\left\{\begin{array}{l}{{x}^{2}-2x+1，x＜0，或x＞2}\\{-{x}^{2}+2x+1，0≤x≤2}\end{array}\right.$，图象如图所示，
（2）y=$\frac{2-x}{x-3}$=-1-$\frac{1}{x-3}$，图象如图所示．
解答 解：（1）y=|x2-2x|+1=$\left\{\begin{array}{l}{{x}^{2}-2x+1，x＜0，或x＞2}\\{-{x}^{2}+2x+1，0≤x≤2}\end{array}\right.$，图象如图所示，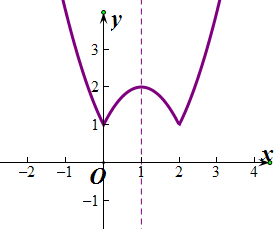
（2）y=$\frac{2-x}{x-3}$=-1-$\frac{1}{x-3}$，图象如图所示（先画出y=-$\frac{1}{x}$的图象，然后向右平移3个单位，向下平移一个单位即可得到y=$\frac{2-x}{x-3}$的图象）．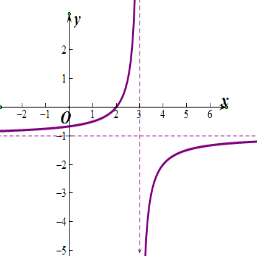
点评 本题考查了绝对值函数的图象的画法，和图象的平移，属于基础题．
练习册系列答案
相关题目
8．
某企业员工有500人参加“学雷锋”志愿活动，按年龄分组：第一组[25，30），第二组[30，35），第三组[35，40），第四组[40，45），第五组[45，50），得到的频率分布直方图如图所示
（Ⅰ）下表是年龄的频数分布表，求正整数a，b的值，
（Ⅱ）现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，年龄在第1，2，3组抽取的人数分别是多少？
某企业员工有500人参加“学雷锋”志愿活动，按年龄分组：第一组[25，30），第二组[30，35），第三组[35，40），第四组[40，45），第五组[45，50），得到的频率分布直方图如图所示 （Ⅰ）下表是年龄的频数分布表，求正整数a，b的值，
| 区间 | [25，30） | [30，35） | [35，40） | [40，45） | [45，50） |
| 人数 | 50 | 50 | a | 150 | b |