题目内容
【题目】已知函数![]() 有两个不同的极值点.
有两个不同的极值点.
(Ⅰ)求实数a的取值范围;
(Ⅱ)若对任意![]() 存在
存在![]() 使得
使得![]() 成立,证明:
成立,证明:![]() .
.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】
(Ⅰ)求得![]() ,令
,令![]() ,得到
,得到![]() ,设
,设![]() ,
,
利用导数求得函数![]() 的单调性与最值,列出不等式组,即可求解;
的单调性与最值,列出不等式组,即可求解;
(Ⅱ)由(Ⅰ)知![]() ,得到
,得到![]() ,把对任意
,把对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,转化为
成立,转化为![]() ,化简
,化简 ,
,
令![]() ,利用导数求得函数
,利用导数求得函数![]() 的单调性与极值,即可求解.
的单调性与极值,即可求解.
(Ⅰ)由函数![]() ,则
,则 ,
,
令![]() ,可得
,可得![]() ,
,
设![]() ,则
,则![]() ,
,
令![]() ,解得
,解得![]() ,
,
列表如下:
|
|
|
|
| + | 0 | - |
| 单调递增 | 单调递减 |
所以![]() 的极大值为
的极大值为![]() ,
,
又因为![]() ,
,
所以函数![]() 有两个不同的极值点等价于
有两个不同的极值点等价于![]() ,解得
,解得![]() ,
,
因此实数![]() 的取值范围为
的取值范围为![]() ;
;
(Ⅱ)由(Ⅰ)知![]() ,故
,故![]() ,
,
设![]() 的较大零点为
的较大零点为![]() ,则
,则![]() ,
,
且![]() ,
,![]() ;
;![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
从而![]() 有最大值为
有最大值为![]() ,
,
又当![]() 时,
时,![]() ,故可设函数
,故可设函数![]() 的值域为
的值域为![]() ,其中
,其中![]() ,
,
由题意:对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,
成立,
等价于![]() ,
,
而![]() ,且
,且![]() ,
,
所以 ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,故
,故![]() ,
,
因此![]() .
.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
【题目】新生儿某疾病要接种三次疫苗免疫(即0、1、6月龄),假设每次接种之间互不影响,每人每次接种成功的概率相等为了解新生儿该疾病疫苗接种剂量与接种成功之间的关系,现进行了两种接种方案的临床试验:10μg/次剂量组与20μg/次剂量组,试验结果如下:
接种成功 | 接种不成功 | 总计(人) | |
10μg/次剂量组 | 900 | 100 | 1000 |
20μg/次剂量组 | 973 | 27 | 1000 |
总计(人) | 1873 | 127 | 2000 |
(1)根据数据说明哪种方案接种效果好?并判断能否有99.9%的把握认为该疾病疫苗接种成功与两种接种方案有关?
(2)以频率代替概率,若选用接种效果好的方案,参与该试验的1000人的成功人数比此剂量只接种一次的成功人数平均提高多少人.
参考公式: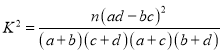 ,其中
,其中![]()
参考附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |