题目内容
已知函数f(x)=tan .
.
(1)求f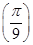 的值;
的值;
(2)设α∈ ,若f
,若f =2,求cos
=2,求cos 的值.
的值.
 .
.(1)求f
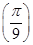 的值;
的值;(2)设α∈
 ,若f
,若f =2,求cos
=2,求cos 的值.
的值.(1)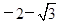 (2)-
(2)-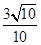
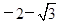 (2)-
(2)-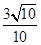
(1)f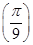 =tan
=tan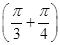 =
=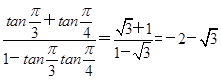 .
.
(2)因为f =tan
=tan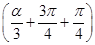 =tan(α+π)=tan α=2,所以
=tan(α+π)=tan α=2,所以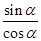 =2,即sin α=2cos α.①又sin2α+cos2α=1,②由①、②解得cos2α=
=2,即sin α=2cos α.①又sin2α+cos2α=1,②由①、②解得cos2α=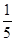 .
.
因为α∈ ,所以cos α=-
,所以cos α=-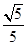 ,sin α=-
,sin α=-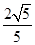 .
.
所以cos =cos αcos
=cos αcos 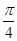 +sin αsin
+sin αsin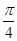 =-
=-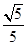 ×
×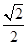 +
+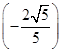 ×
×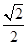 =-
=-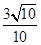 .
.
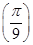 =tan
=tan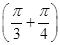 =
=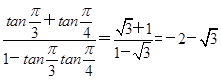 .
.(2)因为f
 =tan
=tan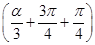 =tan(α+π)=tan α=2,所以
=tan(α+π)=tan α=2,所以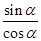 =2,即sin α=2cos α.①又sin2α+cos2α=1,②由①、②解得cos2α=
=2,即sin α=2cos α.①又sin2α+cos2α=1,②由①、②解得cos2α=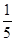 .
.因为α∈
 ,所以cos α=-
,所以cos α=-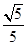 ,sin α=-
,sin α=-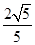 .
.所以cos
 =cos αcos
=cos αcos 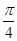 +sin αsin
+sin αsin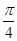 =-
=-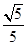 ×
×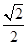 +
+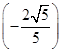 ×
×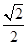 =-
=-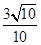 .
.
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
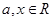 ,函数
,函数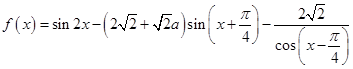 .
.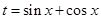 ,将函数
,将函数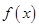 表示为关于
表示为关于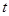 的函数
的函数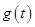 ,求
,求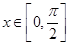 ,不等式
,不等式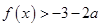 都成立,求实数
都成立,求实数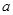 的取值范围.
的取值范围. 则
则 .
.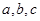 ,若
,若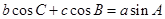 ,则△ABC的形状为( )
,则△ABC的形状为( )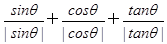 的值是( )
的值是( )
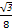
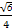
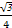
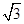 ).
).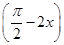 -2f2(x)在区间
-2f2(x)在区间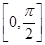 上的值域.
上的值域.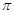
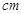 的弧所对的圆心角为
的弧所对的圆心角为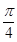 ,则这条弧所在的扇形面积为
,则这条弧所在的扇形面积为 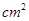 .
.