题目内容
【题目】已知正方体 ABCD-A1B1C1D1 的棱长为 1 , E 、F 分别是棱 AB 、BC上的动点 ,且AE = BF .求直线 A1E 与C1F 所成角的最小值(用反三角函数表示).
【答案】![]()
【解析】
解法 1 :如图, 延长 DC 到点 G, 使得 CG = AE , 联 结C1G 、FG.
由题意知,A1E ∥ C1G, A1E 到C1F 所 成 的 角 等 于∠FC1G .
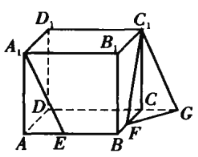
令 AE = CG = x(0≤x≤1), 则有CF =1 - x , C1G =![]() ,
,
![]() .
.
在△C1FG 中, 由余弦定理得![]()
![]() .
.
∠FC1G 取得最小值就是![]() 取得最大值, 亦即
取得最大值, 亦即![]() 取得最小值.
取得最小值.
利用等式![]() ,
,
得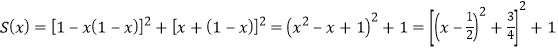 .
.
所以,当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
因此,![]() ,即
,即![]() .
.
故 A1E 与 C1F 所成的最小角为![]() ,此时, E 、F 分别为棱AB 、BC 的中点.
,此时, E 、F 分别为棱AB 、BC 的中点.
解法 2:前面同上, 得到![]() .
.
则![]()
![]() .
.
令![]() ,得
,得![]() .
.
所以, 当![]() 时,
时,![]() 取最小值.
取最小值.
以下与解法 1 同.

练习册系列答案
相关题目
【题目】“互联网![]() ”是“智慧城市”的重要内士,
”是“智慧城市”的重要内士,![]() 市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费
市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费![]() .为了解免费
.为了解免费![]() 在
在![]() 市的使用情况,调査机构借助网络进行了问卷调查,并从参与调査的网友中抽取了
市的使用情况,调査机构借助网络进行了问卷调查,并从参与调査的网友中抽取了![]() 人进行抽样分析,得到如下列联表(单位:人):
人进行抽样分析,得到如下列联表(单位:人):
经常使用免费WiFi | 偶尔或不用免费WiFi | 合计 | |
45岁及以下 | 70 | 30 | 100 |
45岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,判断是否有![]() 的把握认为
的把握认为![]() 市使用免费
市使用免费![]() 的情况与年龄有关;
的情况与年龄有关;
(2)将频率视为概率,现从该市![]() 岁以上的市民中用随机抽样的方法每次抽取
岁以上的市民中用随机抽样的方法每次抽取![]() 人,共抽取
人,共抽取![]() 次.记被抽取的
次.记被抽取的![]() 人中“偶尔或不用免费
人中“偶尔或不用免费![]() ”的人数为
”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列,数学期望
的分布列,数学期望![]() 和方差
和方差![]() .
.
附: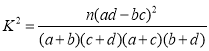 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
