题目内容
14．若a＞b＞1，c＜0，则（ ）| A． | ac＞bc | B． | bc＞c | C． | a|c|＞b|c| | D． | $\frac{a}{c}$＞$\frac{b}{c}$ |
分析 利用不等式的基本性质即可判断出．
解答 解：A．∵a＞b＞1，c＜0，∴ac＜bc，因此A不成立；
B．∵b＞1，c＜0，∴bc＜c，因此不正确；
C．∵a＞b＞1，c＜0，∴a|c|＞b|c|，正确．
D．∵a＞b＞1，c＜0，∴$\frac{a}{c}＜\frac{b}{c}$，故不正确．
故选：C．
点评 本题考查了不等式的基本性质，属于基础题．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
2．
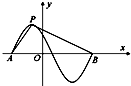函数f（x）=cos（πx+φ）（φ＞0）的图象如图所示，设P是图象的最高点，A、B是图象与x轴的交点，则tan∠APB=（ ）
函数f（x）=cos（πx+φ）（φ＞0）的图象如图所示，设P是图象的最高点，A、B是图象与x轴的交点，则tan∠APB=（ ）| A． | 10 | B． | 8 | C． | $\frac{8}{7}$ | D． | $\frac{4}{7}$ |
如图，AB是⊙O的直径，点C是⊙O上的动点，PA垂直于⊙O所在的平面．
6．为了得到函数$y=sin2x-\sqrt{3}cos2x$的图象，可以将函数y=4sinxcosx的图象（ ）
| A． | 向右平移$\frac{π}{12}$个单位 | B． | 向左平移$\frac{π}{12}$个单位 | ||
| C． | 向右平移$\frac{π}{6}$个单位 | D． | 向左平移$\frac{π}{6}$个单位 |
某校从参加2015年高考的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六组[90，100），[100，110），…，[140，150]后得到部分频率分布直方图（如图所示）．观察图中数据，回答下列问题．
4．已知圆的参数方程为$\left\{\begin{array}{l}x=2+\sqrt{2}cosθ\\ y=1+\sqrt{2}sinθ\end{array}\right.（θ为参数）$，那么该圆的普通方程是（ ）
| A． | ${（x-2）^2}+{（y-1）^2}=\sqrt{2}$ | B． | ${（x+2）^2}+{（y+1）^2}=\sqrt{2}$ | C． | （x-2）2+（y-1）2=2 | D． | （x+2）2+（y+1）2=2 |