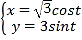题目内容
【题目】如图,在边长为![]() 的菱形
的菱形![]() 中,
中,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,将
,将![]() 沿直线
沿直线![]() 折起到
折起到![]() 的位置(点
的位置(点![]() 不与
不与![]() ,
,![]() 两点重合).
两点重合).

(1)求证:不论![]() 折起到何位置,都有
折起到何位置,都有![]() 平面
平面![]() ;
;
(2)当![]() 平面
平面![]() 时,点
时,点![]() 是线段
是线段![]() 上的一个动点,若
上的一个动点,若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求
,求![]() 的值.
的值.
【答案】(1)详见解析;(2)![]() 或
或![]() .
.
【解析】
(1)由线面垂直的判定定理,即可证明![]() 平面
平面![]() ;
;
(2)用空间向量的方法,以![]() ,
,![]() ,
,![]() 的方向分别为
的方向分别为![]() ,
,![]() ,
,![]() 轴正方向建立空间直角坐标系,设
轴正方向建立空间直角坐标系,设![]() ,用
,用![]() 表示出直线与平面所成角的余弦值,再由
表示出直线与平面所成角的余弦值,再由![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,即可求出结果.
,即可求出结果.
(1)证明:因为四边形![]() 是菱形,所以
是菱形,所以![]() .
.
因为![]() ,点
,点![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
(2)解:以![]() ,
,![]() ,
,![]() 的方向分别为
的方向分别为![]() ,
,![]() ,
,![]() 轴正方向建立空间直角坐标系
轴正方向建立空间直角坐标系![]() 如下图所示.
如下图所示.
易知![]() ,
,![]() ,
,![]() ,
,
则点![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
设![]() ,则
,则![]() .
.
所以![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
由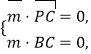 得
得![]() 解得
解得![]()
令![]() ,得平面
,得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以 ,
,
解得![]() .
.
故所求![]() 的值为
的值为![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】某校2011年到2019年参加“北约”“华约”考试而获得加分的学生人数(每位学生只能参加“北约”“华约”中的一种考试)可以通过以下表格反映出来,(为了方便计算,将2011年编号为1,2012年编号为2,依此类推)
年份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
人数y | 2 | 3 | 5 | 4 | 5 | 7 | 8 | 10 | 10 |
(1)求这九年来,该校参加“北约”“华约”考试而获得加分的学生人数的平均数和方差;
(2)根据最近五年的数据,利用最小二乘法求出y与x的线性回归方程,并依此预测该校2020年参加“北约”“华约”考试而获得加分的学生人数.(最终结果精确至个位)
参考数据:回归直线的方程是![]() ,其中
,其中 ,
,![]() ,
,![]() ,
,![]() .
.