题目内容
【题目】如图,在四面体![]() 中,
中,![]() 分别为
分别为![]() 的中点,过
的中点,过![]() 任作一个平面
任作一个平面![]() 分别与直线
分别与直线![]() 相交于点
相交于点![]() ,则下列结论正确的是___________.①对于任意的平面
,则下列结论正确的是___________.①对于任意的平面![]() ,都有直线
,都有直线![]() ,
,![]() ,
,![]() 相交于同一点;②存在一个平面
相交于同一点;②存在一个平面![]() ,使得点
,使得点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 的延长线上; ③对于任意的平面
的延长线上; ③对于任意的平面![]() ,都有
,都有![]() ;④对于任意的平面
;④对于任意的平面![]() ,当
,当![]() 在线段
在线段![]() 上时,几何体
上时,几何体![]() 的体积是一个定值.
的体积是一个定值.

【答案】③④
【解析】
当![]() 分别为
分别为![]() 中点时,可知三线互相平行,排除①;若三线相交,交点必在
中点时,可知三线互相平行,排除①;若三线相交,交点必在![]() 上,可排除②;取
上,可排除②;取![]() 中点
中点![]() ,利用线面平行判定定理可证得
,利用线面平行判定定理可证得![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,再结合
,再结合![]() 为
为![]() 中点可得
中点可得![]() 到平面
到平面![]() 的距离相等,进一步得到
的距离相等,进一步得到![]() 到直线
到直线![]() 的距离相等,从而证得面积相等,③正确;首先通过临界状态
的距离相等,从而证得面积相等,③正确;首先通过临界状态![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合时,求得所求体积为四面体体积一半;当不位于临界状态时,根据③的结论可证得
重合时,求得所求体积为四面体体积一半;当不位于临界状态时,根据③的结论可证得![]() ,从而可知所求体积为四面体体积一半,进而可知为定值,④正确.
,从而可知所求体积为四面体体积一半,进而可知为定值,④正确.
当![]() 分别为
分别为![]() 中点时,
中点时,![]() ,则①错误
,则①错误
若![]() 三线相交,则交点
三线相交,则交点![]()
![]() 不存在
不存在![]() 在线段
在线段![]() 上,
上,![]() 在线段
在线段![]() 延长线上的情况,则②错误
延长线上的情况,则②错误
取![]() 中点
中点![]() ,如图
,如图![]() 所示:
所示:
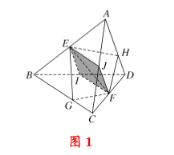
![]() 分别为
分别为![]() 中点
中点 ![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]()
同理可得:![]() 平面
平面![]()
![]() 到平面
到平面![]() 的距离相等;
的距离相等;![]() 到平面
到平面![]() 的距离相等
的距离相等
又![]() 为
为![]() 中点
中点 ![]() 到平面
到平面![]() 的距离相等
的距离相等
![]() 到平面
到平面![]() 的距离相等
的距离相等
连接![]() 交
交![]() 于
于![]() ,则
,则![]() 为
为![]() 中点
中点 ![]() 到
到![]() 距离相等
距离相等
![]() ,则③正确
,则③正确
当![]() 与
与![]() 重合,
重合,![]() 与
与![]() 重合时,此时几何体体积为三棱锥
重合时,此时几何体体积为三棱锥![]() 的体积
的体积
![]() 为
为![]() 中点
中点 ![]() 三棱锥
三棱锥![]() 的体积为四面体
的体积为四面体![]() 体积的一半
体积的一半

当如图![]() 所示时,由③可知
所示时,由③可知![]()
又![]() 为
为![]() 中点
中点 ![]() 到截面的距离相等
到截面的距离相等 ![]()
![]()
![]()
综上所述,几何体![]() 的体积为四面体
的体积为四面体![]() 体积的一半,为定值,则④正确
体积的一半,为定值,则④正确
本题正确结果:③④

练习册系列答案
相关题目