题目内容
17. 如图,四边形ABCD和ADPQ均为正方形,他们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点,设异面直线EM与AF所成的角为θ,则cosθ的最大值为$\frac{2}{5}$.
如图,四边形ABCD和ADPQ均为正方形,他们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点,设异面直线EM与AF所成的角为θ,则cosθ的最大值为$\frac{2}{5}$.
分析 首先以AB,AD,AQ三直线为x,y,z轴,建立空间直角坐标系,并设正方形边长为2,M(0,y,2),从而可求出向量$\overrightarrow{EM},\overrightarrow{AF}$的坐标,由cosθ=$|cos<\overrightarrow{EM},\overrightarrow{AF}>|$得到$cosθ=\frac{2-y}{\sqrt{5}•\sqrt{{y}^{2}+5}}$,对函数$\frac{2-y}{\sqrt{5}•\sqrt{{y}^{2}+5}}$求导,根据导数符号即可判断该函数为减函数,从而求出cosθ的最大值.
解答  解:根据已知条件,AB,AD,AQ三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,设AB=2,则:
解:根据已知条件,AB,AD,AQ三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,设AB=2,则:
A(0,0,0),E(1,0,0),F(2,1,0);
M在线段PQ上,设M(0,y,2),0≤y≤2;
∴$\overrightarrow{EM}=(-1,y,2),\overrightarrow{AF}=(2,1,0)$;
∴cosθ=$|cos<\overrightarrow{EM},\overrightarrow{AF}>|$=$\frac{2-y}{\sqrt{{y}^{2}+5}•\sqrt{5}}$;
设f(y)=$\frac{2-y}{\sqrt{{y}^{2}+5}•\sqrt{5}}$,$f′(y)=\frac{-2y-5}{\sqrt{5}({y}^{2}+5)\sqrt{{y}^{2}+5}}$;
函数g(y)=-2y-5是一次函数,且为减函数,g(0)=-5<0;
∴g(y)<0在[0,2]恒成立,∴f′(y)<0;
∴f(y)在[0,2]上单调递减;
∴y=0时,f(y)取到最大值$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 考查建立空间直角坐标系,利用空间向量解决异面直线所成角的问题,异面直线所成角的概念及其范围,向量夹角的概念及其范围,以及向量夹角余弦的坐标公式,函数导数符号和函数单调性的关系.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案| X | -2 | -1 | 0 | 1 | 2 |
| P | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{5}$ | m | $\frac{1}{20}$ |
(2)求E(X);
(3)若Y=2X-3,求E(Y).
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | 2π |

| A. | 2+$\sqrt{5}$ | B. | 4+$\sqrt{5}$ | C. | 2+2$\sqrt{5}$ | D. | 5 |

| A. | (kπ-$\frac{1}{4}$,kπ+$\frac{3}{4}$,),k∈z | B. | (2kπ-$\frac{1}{4}$,2kπ+$\frac{3}{4}$),k∈z | ||
| C. | (k-$\frac{1}{4}$,k+$\frac{3}{4}$),k∈z | D. | ($2k-\frac{1}{4}$,2k+$\frac{3}{4}$),k∈z |
 为比较甲,乙两地某月14时的气温,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论:
为比较甲,乙两地某月14时的气温,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图,考虑以下结论: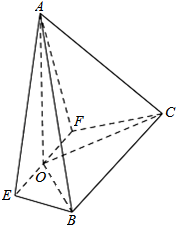 如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.
如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点. 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.