题目内容
7．在等差数列{an}中，若a21+a1000+a2000=30，a1、a2013为方程x2-ax+20=0的两根，则a=（ ）| A． | 5 | B． | 10 | C． | 15 | D． | 20 |
分析 利用等差数列{an}中，a21+a1000+a2000=30，可得a1+1006d=10，再利用韦达定理即可得出结论．
解答 解：∵等差数列{an}中，a21+a1000+a2000=30，
∴3a1+3018d=30，
∴a1+1006d=10，
∴a1+a2013=2（a1+1006d）=20，
∵a1、a2013为方程x2-ax+20=0的两根，
∴a1+a2013=a，
∴a=20，
故选：D．
点评 本题考查根与系数的关系，考查等差数列，确定方程的根是关键．
练习册系列答案
相关题目
2．定义：如果函数f（x）在[a，b]上存在x1，x2（a＜x1＜x2＜b）满足f′（x1）=$\frac{f（b）-f（a）}{b-a}$，f′（x2）$\frac{f（b）-f（a）}{b-a}$，则称函数f（x）是[a，b]上的“双中值函数”．已知函数f（x）=x3-x2+a是[0，a]上“双中值函数”，则实数a的取值范围是（ ）
| A． | （$\frac{1}{3}$，$\frac{1}{2}$） | B． | （0，1） | C． | （$\frac{1}{3}$，1） | D． | （$\frac{1}{2}$，1） |
12．设（1+x）3+（1+x）4+…+（1+x）50=a0+a1x+a2x2+…+a50x50，则a3等于（ ）
| A． | C${\;}_{51}^{3}$ | B． | C${\;}_{51}^{4}$ | C． | 2C${\;}_{50}^{3}$ | D． | C${\;}_{50}^{4}$ |
19．已知实数a，b，c满足$\frac{1}{4}$a2+$\frac{1}{4}$b2+c2=1，则ab+2bc+2ca的取值范围是（ ）
| A． | （-∞，4] | B． | [-4，4] | C． | [-2，4] | D． | [-1，4] |
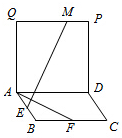如图，四边形ABCD和ADPQ均为正方形，他们所在的平面互相垂直，动点M在线段PQ上，E、F分别为AB、BC的中点，设异面直线EM与AF所成的角为θ，则cosθ的最大值为$\frac{2}{5}$．