Question

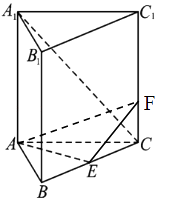
【题目】如图，平面ABEF⊥平面ABC，四边形ABEF为矩形，AC=BC．O为AB的中点，OF⊥EC．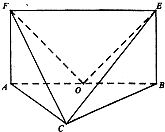

（1）求证：OE⊥FC：
（2）若 时，求二面角F﹣CE﹣B的余弦值．

Answer 1

【答案】
（1）证明：连结OC，∵AC=BC，O是AB的中点，

故OC⊥AB．

又∵平面ABC⊥平面ABEF，

故OC⊥平面ABE，于是OC⊥OF．

又OF⊥EC，∵OF⊥平面OEC，

∴OF⊥OE，

又∵OC⊥OE，∴OE⊥平面OFC，

∴OE⊥FC；

（2）解：由（1）得AB=2AF．不妨设AF=1，AB=2，

∵ ，∴AC= ，则OC=

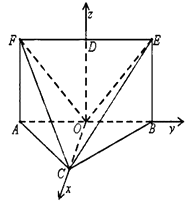
建立以O为坐标原点，OC，OB，OD分别为x，y，z轴的空间直角坐标系如图：

则F（0，﹣1，1），E（0，1，1），B（0，1，0），C（ ，0，0），则

=（﹣ ，1，1）， =（0，﹣2，0），

设平面FCE的法向量为 =（x，y，z），

则 ．

∴ =（1，0， ），

∵ =（0，0，1）， =（ ，﹣1，0），

∴同理可得平面CEB的法向量为 =（1， ，0），

∴cos＜ ， ＞= = ，

∵二面角F﹣CE﹣B是钝二面角，

∴二面角F﹣CE﹣B的余弦值为﹣ ．

【解析】（1）连结OC，则OC⊥AB，从而得到OC⊥OF，进而得到OF⊥OE，由此能证明OE⊥FC．（2）由（1）得AB=2AF．不妨设AF=1，AB=2建立空间坐标系，求出平面的法向量，利用向量法即可．
【考点精析】通过灵活运用直线与平面垂直的性质，掌握垂直于同一个平面的两条直线平行即可以解答此题．