题目内容
【题目】已知函数f(x)=(1﹣m)lnx+ ![]() ﹣x,m∈R且m≠0.
﹣x,m∈R且m≠0.
(Ⅰ)当m=2时,令g(x)=f(x)+log2(3k﹣1),k为常数,求函数y=g(x)的零点的个数;
(Ⅱ)若不等式f(x)>1﹣ ![]() 在x∈[1,+∞)上恒成立,求实数m的取值范围.
在x∈[1,+∞)上恒成立,求实数m的取值范围.
【答案】解:(Ⅰ)当m=2时,g(x)=﹣lnx+x2﹣x+log2(3k﹣1),x>0,
所以 ![]() ,
,
令g'(x)=0,解得x=1或 ![]() (舍去),
(舍去),
当x∈(0,1)时,g'(x)<0,所以y=g(x)在(0,1)上单调递减,
当x∈(1,+∞)时,g'(x)>0,所以y=g(x)在(1,+∞)上单调递增,
所以x=1是y=g(x)的极小值点,y=g(x)的最小值为g(1)=log2(3k﹣1)…(3分)
当log2(3k﹣1)=0,即 ![]() 时,函数y=g(x)有一个零点,
时,函数y=g(x)有一个零点,
当log2(3k﹣1)>0,即 ![]() 时,函数y=g(x)没有零点,
时,函数y=g(x)没有零点,
当log2(3k﹣1)<0,即 ![]() 时,函数y=g(x)有两个零点
时,函数y=g(x)有两个零点
(Ⅱ)由已知  ,
,
令f'(x)=0,解得 ![]() ,由于
,由于 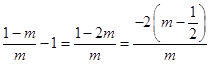 ,
,
①若m<0,则 ![]() ,故当x≥1时,f'(x)≤0,因此f(x)在[1,+∞)上单调递减,
,故当x≥1时,f'(x)≤0,因此f(x)在[1,+∞)上单调递减,
所以 ![]() ,又因为
,又因为 ![]() ,则
,则 ![]() 不成立
不成立
②若 ![]() ,则
,则 ![]() ,故当
,故当 ![]() 时,f'(x)≤0;当
时,f'(x)≤0;当 ![]() 时,f'(x)>0,
时,f'(x)>0,
即f(x)在 ![]() 上单调递减,在
上单调递减,在 ![]() 上单调递增,
上单调递增,
所以  ,
,
因为 ![]() ,所以
,所以 ![]() ,
,
则 ![]() ,
,
因此当 ![]() 时,
时, ![]() 恒成立
恒成立
③若 ![]() ,则
,则 ![]() ,故当x≥1时,f'(x)≥0,
,故当x≥1时,f'(x)≥0,
因此f(x)在[1,+∞)上单调递增,
故 ![]() ,令
,令 ![]() ,化简得m2﹣4m+2>0,
,化简得m2﹣4m+2>0,
解得 ![]() ,所以
,所以 ![]()
综上所述,实数m的取值范围是 ![]()
【解析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的零点个数即可;(Ⅱ)求出函数的导数,通过讨论m的范围,得到函数的单调区间,从而求出函数f(x)的最小值,确定m的范围即可.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案