题目内容
【题目】已知椭圆C: ![]() 的上、下焦点分别为F1 , F2 , 上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e=
的上、下焦点分别为F1 , F2 , 上焦点F1到直线 4x+3y+12=0的距离为3,椭圆C的离心率e= ![]() .
. 
(I)若P是椭圆C上任意一点,求| ![]() ||
|| ![]() |的取值范围;
|的取值范围;
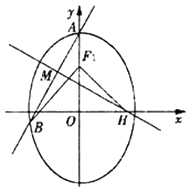
(II)设过椭圆C的上顶点A的直线l与椭圆交于点B(B不在y轴上),垂直于l的直线与l交于点M,与x轴交于点H,若 ![]() =0,且|
=0,且| ![]() |=|
|=| ![]() |,求直线l的方程.
|,求直线l的方程.
【答案】解:(Ⅰ)由已知椭圆C方程为 ![]() ,
,
设椭圆上焦点F1(0,c),由F1到直线4x+3y+12=0的距离为3,
得 ![]() ,又椭圆C的离心率
,又椭圆C的离心率 ![]() ,所以
,所以 ![]() ,又a2=b2+c2,
,又a2=b2+c2,
求得a2=4b2=3.椭圆C方程为 ![]() ,
,
所以1≤|PF1|≤3,设 ![]() ,
, ![]() =﹣(t﹣2)2+4,t=2时,
=﹣(t﹣2)2+4,t=2时,
![]() 最大值为4,t=1或3时,
最大值为4,t=1或3时, ![]() 最小值为3,
最小值为3,
![]() 取值范围是[3,4].…(5分)
取值范围是[3,4].…(5分)
(Ⅱ)设直线l的斜率为k,
则直线l方程y﹣2=kx,设B(xB,yB),A(xA,yA),
由 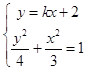 ,得(3k2+4)x2+12kx=0,
,得(3k2+4)x2+12kx=0,
则有xA=0, ![]() ,所以
,所以 ![]() ,
,
所以 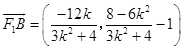 ,
, ![]() ,
,
由已知 ![]() ,
,
所以 ![]() ,解得
,解得 ![]() ,
, ![]() ,
,
![]() ,yM=1,MH的方程
,yM=1,MH的方程  ,联立
,联立 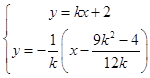 ,
,
 ,解得
,解得 ![]() ,
,
所以线l的方程为 ![]()
【解析】(Ⅰ)设椭圆上焦点F1(0,c),由F1到直线4x+3y+12=0的距离为3,结合椭圆C的离心率 ![]() ,求出椭圆C方程,推出1≤|PF1|≤3,设
,求出椭圆C方程,推出1≤|PF1|≤3,设 ![]() ,
, ![]() =﹣(t﹣2)2+4,t=2时,然后求解
=﹣(t﹣2)2+4,t=2时,然后求解 ![]() 取值范围.(Ⅱ)设直线l的斜率为k,直线l的方程y﹣2=kx,设B(xB,yB),A(xA,yA),联立直线与椭圆方程,求出A,B坐标,利用
取值范围.(Ⅱ)设直线l的斜率为k,直线l的方程y﹣2=kx,设B(xB,yB),A(xA,yA),联立直线与椭圆方程,求出A,B坐标,利用 ![]() ,求出H、M的坐标,推出k即可求出直线l的方程.
,求出H、M的坐标,推出k即可求出直线l的方程.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.

 智慧小复习系列答案
智慧小复习系列答案【题目】为研究男女同学空间想象能力的差异,孙老师从高一年级随机选取了20名男生、20名女生,进行空间图形识别测试,得到成绩茎叶图如下,假定成绩大于等于80分的同学为“空间想象能力突出”,低于80分的同学为“空间想象能力正常”. 
(1)完成下面2×2列联表,
空间想象能力突出 | 空间想象能力正常 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
(2)判断是否有90%的把握认为“空间想象能力突出”与性别有关;
(3)从“空间想象能力突出”的同学中随机选取男生2名、女生2名,记其中成绩超过90分的人数为ξ,求随机变量ξ的分布列和数学期望. 下面公式及临界值表仅供参考: ![]()
P(X2≥k) | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | 6.635 |