题目内容
【题目】等差数列{an}的前n项和为Sn , 且a3=9,S6=60.
(I)求数列{an}的通项公式;
(II)若数列{bn}满足bn+1﹣bn=an(n∈N+)且b1=3,求数列 ![]() 的前n项和Tn .
的前n项和Tn .
【答案】解:(Ⅰ)设等差数列{an}的公差为d,∵a3=9,S6=60.
∴ 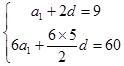 ,解得
,解得 ![]() .
.
∴an=5+(n﹣1)×2=2n+3.
(Ⅱ)∵bn+1﹣bn=an=2n+3,b1=3,
当n≥2时,bn=(bn﹣bn﹣1)+…+(b2﹣b1)+b1
=[2(n﹣1)+3]+[2(n﹣2)+3]+…+[2×1+3]+3= ![]() .
.
当n=1时,b1=3适合上式,所以 ![]() .
.
∴ ![]() .
.
∴ ![]()
= ![]()
= ![]()
【解析】(Ⅰ)设等差数列{an}的公差为d,运用等差数列的通项公式和求和公式,列方程,解方程即可得到首项和公差,即可得到所求通项;(Ⅱ)运用数列的恒等式:当n≥2时,bn=(bn﹣bn﹣1)+…+(b2﹣b1)+b1,结合等差数列的求和公式,检验n=1也成立,再由 ![]() ,运用数列的求和方法:裂项相消求和,化简整理即可得到所求和.
,运用数列的求和方法:裂项相消求和,化简整理即可得到所求和.
【考点精析】关于本题考查的等差数列的通项公式(及其变式)和数列的前n项和,需要了解通项公式:![]() 或
或![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系 才能得出正确答案.
才能得出正确答案.

练习册系列答案
相关题目

