��Ŀ����
����Ŀ������ ![]() ͼ���ϲ�ͬ����
ͼ���ϲ�ͬ���� ![]() ��
�� ![]() �����ߵ�б�ʷֱ���
�����ߵ�б�ʷֱ��� ![]() ��
�� ![]() ���涨
���涨 ![]() ��
�� ![]() Ϊ�߶�
Ϊ�߶� ![]() �ij��ȣ���������
�ij��ȣ��������� ![]() �ڵ�
�ڵ� ![]() ��
�� ![]() ֮��ġ������ȡ��������������⣺
֮��ġ������ȡ��������������⣺
�ٺ��� ![]() ͼ��������
ͼ�������� ![]() ��
�� ![]() �ĺ�����ֱ�Ϊ1��2����
�ĺ�����ֱ�Ϊ1��2���� ![]() ��
��
�ڴ��������ĺ�����ͼ������������֮��ġ������ȡ�Ϊ������
����� ![]() ��
�� ![]() ��������
�������� ![]() �ϲ�ͬ�����㣬��
�ϲ�ͬ�����㣬�� ![]() ��
��
�������� ![]() ��
�� ![]() ����Ȼ�����ĵ������ϲ�ͬ����
����Ȼ�����ĵ������ϲ�ͬ���� ![]() ��
�� ![]() ����
���� ![]() ����
���� ![]() ���������ʵ��
���������ʵ�� ![]() ��ȡֵ��Χ��
��ȡֵ��Χ�� ![]() ��
��
��������������Ϊ�����������������Ŷ����ϣ�
���𰸡��ڢ�
���������⣺���ڢ٣��� ![]() ��
�� ![]() ��
��
�� ![]() ��
��
�� ![]() ����
���� ![]() ��
��
�� ![]() ���ʢٴ���
���ʢٴ���
���ڢڣ���������y=1����ͼ������������֮��ġ������ȡ�Ϊ�������ʢ���ȷ��
���ڢۣ��� ![]() ��
�� ![]() ����
���� ![]() ��
��
�� ![]()
![]() ��
��
�� ![]() ���ʢ���ȷ��
���ʢ���ȷ��
���ڢܣ��� ![]() �ɵ�
�ɵ� ![]() ��
�� 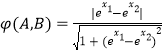 ��
��
�� ![]() ������ɵ�
������ɵ� ![]() �������
�������
���� ![]() ʱ��ʽ��������ʢܴ���
ʱ��ʽ��������ʢܴ���
���Ͽɵâڢ���ȷ��
�ʴ�Ϊ���ڢ�
������Ҫ���麯����ͼ�������ߵļ����ʼ�������ȡֵ��Χ��

 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�����Ŀ�������������ҹ��ڽ��������ϵ�Ͷ�벻�ϼӴ�ѧ�����õ�Ѹ�ͷ�չ��������ҵ�Ĺ��ʾ������õ��������.�����Ź����г����ٷŻ�������ȷʵ����ҵ���к��Ⲽ�֣��ڶ�����ҵ���������������������ֻ���ҵ������Ʒ�����ڸϳ������ͷ��ijƷ���ֻ���˾һֱĬĬ��չ�����г����ں����30�����֧��������Ҫ���ڹ�˾���ɴ���70��80��������Ա��������ҵΪ�˽������������Ա���Ƿ�Ը�ⱻ����������̬�ȣ����ֲ�����ķ�ʽ��70����80���Ա�������������100λ���õ��������±���
Ը�ⱻ���� | ��Ը�ⱻ���� | �ϼ� | |
70�� | 20 | 20 | 40 |
80�� | 40 | 20 | 60 |
�ϼ� | 60 | 40 | 100 |
�ο����ݣ�
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
���ο���ʽ�� ![]() ������
������ ![]() ��
��
��1�����ݲ�����ݣ��Ƿ��� ![]() �İ�����Ϊ���Ƿ�Ը�ⱻ�����������йء�����˵�����ɣ�
�İ�����Ϊ���Ƿ�Ը�ⱻ�����������йء�����˵�����ɣ�
��2���ù�˾�ι�פ�����֧�����Ľ����������ⰲ��4����������70��Ա���μӣ�70���Ա������Ը�ⱻ���ɵ�3�˺Ͳ�Ը�ⱻ���ɵ�3�˱����μӣ��ֲ���������������ӱ�����Ա����ѡ4�ˣ���ѡ��Ը�ⱻ�������������ڲ�Ը�ⱻ���������ĸ���.