题目内容
【题目】如图直三棱柱 ![]() 中,
中, ![]() 为边长为2的等边三角形,
为边长为2的等边三角形, ![]() ,点
,点 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 分别是边
分别是边 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 的中点,动点
的中点,动点 ![]() 在四边形
在四边形 ![]() 内部运动,并且始终有
内部运动,并且始终有 ![]() 平面
平面 ![]() ,则动点
,则动点 ![]() 的轨迹长度为( )
的轨迹长度为( )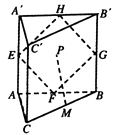
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】因为 ![]() 分别为
分别为 ![]() 的中点,所以
的中点,所以 ![]() ,
, ![]() ,所以
,所以 ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,又因为
,又因为 ![]() ,所以平面
,所以平面 ![]() 平面
平面 ![]() ,要使
,要使 ![]() 平面
平面 ![]() ,则
,则 ![]() 平面
平面 ![]() ,所以点
,所以点 ![]() 的轨迹为线段
的轨迹为线段 ![]() ,点
,点 ![]() 的轨迹长度为
的轨迹长度为 ![]() .
.
故本题正确答案为 ![]() .
.
因为 H , F , M 分别为 A ' B ' , A B , B C 的中点,连接HF,FM,HM, 所以 F M / / A C , H F / / A A ' ,所以 F M / / 平面 A C C ' A ' , H F / / 平面 A C C ' A ' ,又因为 F M ∩ H F = F ,所以平面 H F M / / 平面 A C C ' A ' ,P![]() 平面HFM, 所以MP / / 平面 A C C ' A ' ,所以点 P 的轨迹为线段 H F ,HF=4,所以选D.
平面HFM, 所以MP / / 平面 A C C ' A ' ,所以点 P 的轨迹为线段 H F ,HF=4,所以选D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目