题目内容
【题目】如图,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() //
// ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(1)求证: ![]() ;
;
(2)求证: ![]() //平面
//平面![]() ;
;
(3)求二面角![]() 的大小.
的大小.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】试题分析:(1)以![]() 为原点,分别以
为原点,分别以![]() 、
、![]() 、
、![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向建立空间直角坐标系.求出相关点的坐标,通过计算
轴的正方向建立空间直角坐标系.求出相关点的坐标,通过计算![]() ,证明
,证明![]() ;(2)取
;(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,证明
,证明![]() ,然后证明
,然后证明![]() 平面
平面![]() ;(3)求出平面
;(3)求出平面![]() 的一个法向量,平面
的一个法向量,平面![]() 的法向量,利用空间向量的数量积求解二面角
的法向量,利用空间向量的数量积求解二面角![]() 的余弦值.
的余弦值.
试题解析:(1)证明:依题意, ![]() 平面
平面![]() ,如图,以
,如图,以![]() 为原点,分别以
为原点,分别以![]() 、
、![]() 、
、![]() 的方向为
的方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向建立空间直角坐标系.
轴的正方向建立空间直角坐标系.
依题意,可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,因为
,因为![]() ,
, ![]() ,所以
,所以![]() .
.

所以![]() .
.
(2)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
因为![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,所以
,所以![]() .
.
又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(3)解:因为![]() ,
, ![]() ,
,
![]() ,
,
所以![]() 平面
平面![]() ,故
,故![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
设平面![]() 的法向量为
的法向量为![]() ,
,
因为![]() ,
, ![]() ,
,
所以![]() 即
即![]()
令![]() ,得
,得![]() ,
, ![]() ,故
,故![]() .
.
所以![]() ,所以二面角
,所以二面角![]() 的大小为
的大小为![]() .
.

 阅读快车系列答案
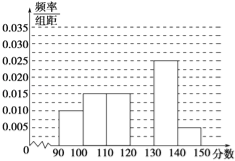
阅读快车系列答案【题目】为了解某校学生参加社区服务的情况,采用按性别分层抽样的方法进行调查.已知该校共有学生960人,其中男生560人,从全校学生中抽取了容量为![]() 的样本,得到一周参加社区服务的时间的统计数据好下表:
的样本,得到一周参加社区服务的时间的统计数据好下表:
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关?
(Ⅲ)以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率,现从该校学生中随机调查6名学生,试估计6名学生中一周参加社区服务时间超过1小时的人数.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]()
【题目】下表提供了工厂技术改造后某种型号设备的使用年限x和所支出的维修费y(万元)的几组对照数据:
x(年) | 2 | 3 | 4 | 5 | 6 |
y(万元) | 1 | 2.5 | 3 | 4 | 4.5 |
(1)若知道y对x呈线性相关关系,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?参考公式: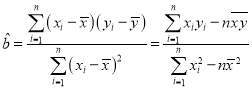 ,
,![]() .
.
【题目】某市环保部门为了让全市居民认识到冬天烧煤取暖对空气![]() 数值的影响,进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数
数值的影响,进而唤醒全市人民的环保节能意识。对该市取暖季烧煤天数![]() 与空气
与空气![]() 数值不合格的天数
数值不合格的天数![]() 进行统计分析,得出下表数据:
进行统计分析,得出下表数据:
| 9 | 8 | 7 | 5 | 4 |
| 7 | 6 | 5 | 3 | 2 |
(1)以统计数据为依据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)求出的线性回归方程,预测该市烧煤取暖的天数为20时空气![]() 数值不合格的天数.
数值不合格的天数.
参考公式: ,
,![]() .
.