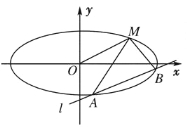
题目内容
【题目】已知圆E经过M(﹣1,0),N(0,1),P(![]() ,
,![]() )三点.
)三点.
(1)求圆E的方程;
(2)若过点C(2,2)作圆E的两条切线,切点分别是A,B,求直线AB的方程.
【答案】(1)x2+y2=1;(2)2x+2y﹣1=0.
【解析】
(1)根据题意,设圆E的圆心E坐标为(a,b),半径为r,结合题意可得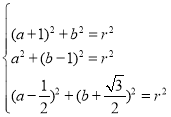 ,解可得a、b、r的值,由圆的标准方程的形式分析可得答案.
,解可得a、b、r的值,由圆的标准方程的形式分析可得答案.
(2)设以C为圆心,CA为半径的圆C,其半径为R,由切线长公式计算可得R的值,分析可得圆C的方程,又由直线AB为圆E与圆C的公共弦所在的直线,联立两个圆的方程,变形分析可得答案.
(1)根据题意,设圆E的圆心E坐标为(a,b),半径为r,
则有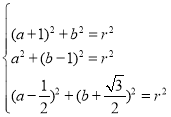 ,解可得
,解可得![]() ,
,
则圆E的方程为x2+y2=1;
(2)根据题意,过点C(2,2)作圆E的两条切线,切点分别是A,B,
设以C为圆心,CA为半径的圆C,其半径为R,
则有R=|CA|![]() ,
,
则圆C的方程为(x﹣2)2+(y﹣2)2=7,即x2+y2﹣4x﹣4y+1=0,
又由直线AB为圆E与圆C的公共弦所在的直线,
则有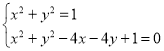 ,
,
解可得2x+2y﹣1=0,
则AB的方程为:2x+2y﹣1=0.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目