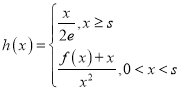题目内容
【题目】设![]() (
(![]() 、
、![]() 为实常数).
为实常数).
(1)当![]() 时,证明:
时,证明:![]() 不是奇函数;
不是奇函数;
(2)设![]() 是奇函数,求
是奇函数,求![]() 与
与![]() 的值;
的值;
(3)当![]() 是奇函数时,研究是否存在这样的实数集的子集
是奇函数时,研究是否存在这样的实数集的子集![]() ,对任何属于
,对任何属于![]() 的
的![]() 、
、![]() ,都有
,都有![]() 成立?若存在试找出所有这样的
成立?若存在试找出所有这样的![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)证明见解析;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)举出反例即可,只要检验![]() ,可说明
,可说明![]() 不是奇函数;
不是奇函数;
(2)由题意可得![]() ,即
,即![]() 对定义域内任意实数
对定义域内任意实数![]() 成立.整理可求
成立.整理可求![]() 、
、![]() ;
;
(3)当![]() 时,
时,![]() ,由指数函数的性质可求
,由指数函数的性质可求![]() ,由二次函数的性质可求
,由二次函数的性质可求![]() ,可求当
,可求当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,结合二次函数的性质可求
,结合二次函数的性质可求![]() 的范围,即可求解.
的范围,即可求解.
(1)举出反例即可:![]() ,
,![]() ,
,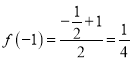 ,
,
所以![]() ,函数
,函数![]() 不是奇函数;
不是奇函数;
(2)![]() 是奇函数时,
是奇函数时,![]() ,
,
即![]() 对定义域内任意实数
对定义域内任意实数![]() 成立.
成立.
化简整理得![]() ,这是关于
,这是关于![]() 的恒等式,
的恒等式,
所以![]() 所以
所以![]() 或
或![]() ,经检验都符合题意;
,经检验都符合题意;
(2)当![]() 时,
时,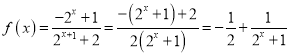 ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,从而
,从而![]() ;
;
而![]() 对任何实数
对任何实数![]() 成立;
成立;
所以可取![]() 对任何
对任何![]() 、
、![]() 属于
属于![]() ,都有
,都有![]() 成立.
成立.
当![]() 时,
时,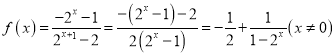 ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
①因此取![]() ,对任何
,对任何![]() 、
、![]() 属于
属于![]() ,都有
,都有![]() 成立;
成立;
②当![]() 时,
时,![]() ,解不等式
,解不等式![]() 得:
得:![]() .
.
所以取![]() ,对任何属于
,对任何属于![]() 的
的![]() 、
、![]() ,都有
,都有![]() 成立.
成立.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目