Question

【题目】已知等比数列的公比，且，是、的等差中项.

（1）求数列的通项公式；

（2）试比较与的大小，并说明理由；

（3）若数列满足，在每两个与之间都插入个2，使得数列变成了一个新的数列，试问：是否存在正整数，使得数列的前项和？如果存在，求出的值；如果不存在，说明理由.

Answer 1

【答案】（1）（2）,详见解析（3）存在，使得

【解析】

（1）根据条件列出方程组，解基本量即可.（2）由（1）可知通项为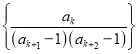：，对通项裂项可得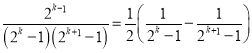：，从而可求出前n项和，即可比较出大小关系.（3）由（2）可知：数列中含有 含有个2，所以数列中，的前所有项之和为，求出S，代入k的具体值，可知当时，，当时，，所以在的基础之上加上471个2可得，把前面所有项的个数加起来即可得到m的值.

解：（1）由是，的等差中项，得，

∴,解得.

∴，从而，

∵，∴解得.

∴，从而.

（2）由（1）知.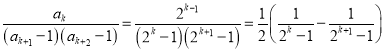

∴

（3）.

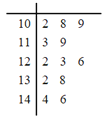
根据题意，数列中，（含项）前的所有项的和为：

.

当时，，

当时，，

又∵,

∴时，，

∴存在，使得.