题目内容
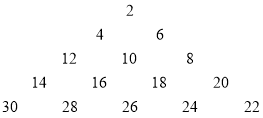
【题目】现有![]() 行数表如下:
行数表如下:
第一行:![]()
第二行:![]()
第三行:![]()
…… …… ……
第![]() 行:
行:![]()
第m行:![]()
按照上述方式从第一行写到第m行(写下的第n个数记作![]() )得到有穷数列
)得到有穷数列![]() ,其前n项和为
,其前n项和为![]() ,若
,若![]() 存在,则
存在,则![]() 的最小值为______
的最小值为______
【答案】![]()
【解析】
观察已知可得每行是以1为首项,以2为公比的等比数列,先判断第2018个数的位置,再利用等比数列的和及分组求和求得![]() .
.
设共有m行,由题意从第一行到第m行,若![]() 存在,则有穷数列
存在,则有穷数列![]() 的项数必须大于等于2018,又第一行共有m个数,第二行共有m-1个数,第三行共有m-2个数,
的项数必须大于等于2018,又第一行共有m个数,第二行共有m-1个数,第三行共有m-2个数,
![]() ,第m行有1个数
,第m行有1个数
则共有1+2+3+![]() +m
+m![]() 2018,
2018,
则m![]() ,当m
,当m![]() 时,则这64行共有2080个数,
时,则这64行共有2080个数,
∴第2018个数位于第54行第4个数,
又由于每行的数构成以1为首项,以2为公比的等比数列,
∴第i行的数的和为![]() ,(i=1,2,3
,(i=1,2,3![]() 64)
64)
∴![]()
=![]() ,
,
故答案为:![]() .
.

【题目】某地区2020年清明节前后3天每天下雨的概率为60%,通过模拟实验的方法来计算该地区这3天中恰好有2天下雨的概率:用随机数![]() (
(![]() ,且
,且![]() )表示是否下雨:当
)表示是否下雨:当![]() 时表示该地区下雨,当
时表示该地区下雨,当![]() 时,表示该地区不下雨,从随机数表中随机取得20组数如下
时,表示该地区不下雨,从随机数表中随机取得20组数如下
332 714 740 945 593 468 491 272 073 445
992 772 951 431 169 332 435 027 898 719
(1)求出![]() 的值,并根据上述数表求出该地区清明节前后3天中恰好有2天下雨的概率;
的值,并根据上述数表求出该地区清明节前后3天中恰好有2天下雨的概率;
(2)从2011年开始到2019年该地区清明节当天降雨量(单位:![]() )如下表:(其中降雨量为0表示没有下雨).
)如下表:(其中降雨量为0表示没有下雨).
时间 | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 | 2019年 |
年份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
降雨量 | 29 | 28 | 26 | 27 | 25 | 23 | 24 | 22 | 21 |
经研究表明:从2011年开始至2020年, 该地区清明节有降雨的年份的降雨量![]() 与年份
与年份![]() 成线性回归,求回归直线
成线性回归,求回归直线![]() ,并计算如果该地区2020年(
,并计算如果该地区2020年(![]() )清明节有降雨的话,降雨量为多少?(精确到0.01)
)清明节有降雨的话,降雨量为多少?(精确到0.01)
参考公式: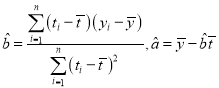 .
.
参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() .
.