Question

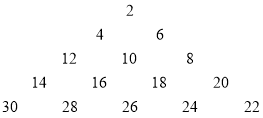
【题目】已知从2开始的连续偶数蛇形排列形成宝塔形数表，第一行为2，第一行为46，第三行为12，10，8，第四行为14，16，18，20.如图所示，在宝塔形数表中位于第i行，第j列的数记为，比如，，，，若，则（ ）

A.65B.70C.71D.72

Answer 1

【答案】C

【解析】

由题意正偶数为等差数列，由图摆放找每一行所放的数，及每一行的数字总数与本数列的每一项的关系即可发现规律

解：由图可知，第一行放1个偶数，第二行放2个偶数，第3行放3个偶数…
又因为指图中摆放的第行第列，
所以先求第行的最后一个偶数，
该偶数小于2020且是最接近的，并且还能成为每一行最后一个数字的，

，

当时，，

第44行的最后一偶数是1980，又第45行的第45个偶数为1982，
利用等差数列的任意两项之间关系可知2020应出在该行的第45-19=26列，故，
所以．
故选：C．