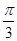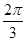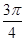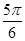题目内容
 ,
,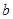 ,
, 分别是△ABC的角
分别是△ABC的角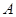 ,
,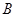 ,
, 的对边,
的对边, ,
,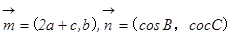 且
且 .
.(1)求角
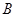 的大小; (2)若
的大小; (2)若 ,
, ,求
,求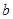 的值.
的值.(1)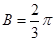 ;(2)
;(2)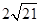
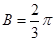 ;(2)
;(2)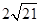
试题分析:(1)由向量数量积的坐标运算可得
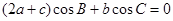 ,利用余弦定理把角化为边或正弦定理把边化成角即可;(2)把条件代入
,利用余弦定理把角化为边或正弦定理把边化成角即可;(2)把条件代入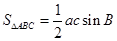 可求得边
可求得边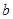 。
。(1)法一;由
 ,得
,得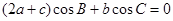 ,
, 由余弦定理得
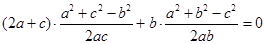 ,
, 化简得
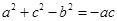 ,
,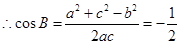 ,
,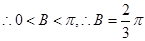 。
。法二:由
 , 得
, 得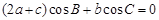 ,即
,即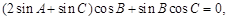
即
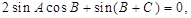 即
即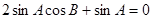 ,
,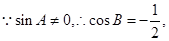 又
又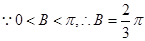 。
。(2)由
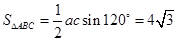 得
得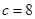 。
。由余弦定理得
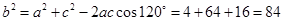 ,即
,即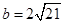 。
。 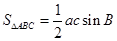 的逆用。
的逆用。
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
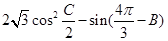 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小.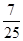
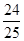
 ,求角A;(2)若
,求角A;(2)若 ,求△ABC的面积.
,求△ABC的面积.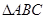 的内角满足
的内角满足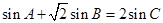 ,则
,则 的最小值是 .
的最小值是 .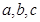 分别为
分别为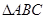 三个内角
三个内角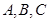 的对边,且
的对边,且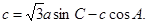
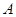 ;
;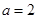 ,△ABC的面积为
,△ABC的面积为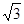 ,求
,求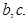
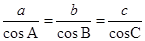 , 那么△ABC是( )
, 那么△ABC是( )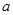 ,
,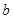 ,
,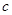 .若
.若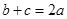 ,
,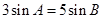 ,则角
,则角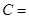 ( )
( )