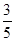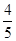题目内容
在△ABC中,a、b、c分别为角A、B、C所对的边,且(2b+c)cosA十acosC =0。
(1)求角A的大小;
(2)求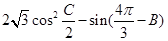 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小.
(1)求角A的大小;
(2)求
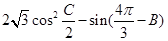 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小.(1)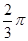 ;(2)
;(2) 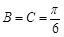 .
.
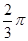 ;(2)
;(2) 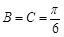 .
.试题分析:(1)此类解三角形的问题,主要使用正余弦定理,将边角互化,对于第一问,通过观察,利用余弦定理,可将
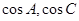 化简,转化成边的关系,然后利用
化简,转化成边的关系,然后利用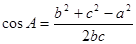 ,得到角A的大小;
,得到角A的大小;(2)通过公式
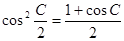 ,将角
,将角 转化成角
转化成角 ,利用两角和的正弦公式展开,化一,得到原式
,利用两角和的正弦公式展开,化一,得到原式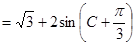 ,根据角
,根据角 的范围,结合三角函数的图像,当
的范围,结合三角函数的图像,当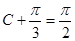 时,取得最大值,得到此时的角
时,取得最大值,得到此时的角 的大小,此题属于基础题型.
的大小,此题属于基础题型.试题解析:
 ,所以由余弦定理得
,所以由余弦定理得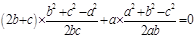 ,
,化简整理得
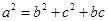 ,由余弦定理得
,由余弦定理得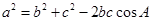 , 4分
, 4分所以
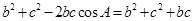 ,即
,即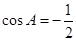 ,又
,又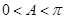 ,所以
,所以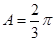 6分
6分(2)∵
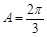 ,∴
,∴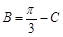 ,
,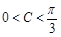 .
.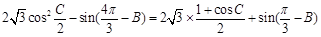
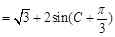 8分
8分∵
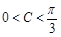 ,∴
,∴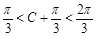 ,∴当
,∴当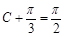 ,
,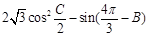 取最大值
取最大值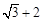 ,此时
,此时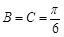 . 12分
. 12分
练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
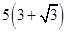 海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距
海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距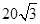 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?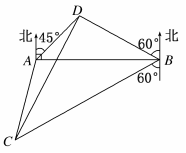
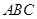 中,已知
中,已知 ,向量
,向量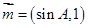 ,
,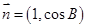 ,且
,且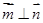 .
.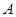 的值;
的值;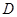 在边
在边 上,且
上,且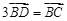 ,
,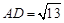 ,求△
,求△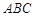 的面积.
的面积. ( )
( )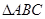 中,角
中,角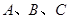 所对的边分别为
所对的边分别为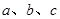 ,那么下列给出的各组条件能确定三角形有两解的是( )
,那么下列给出的各组条件能确定三角形有两解的是( )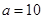 ,
,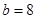 ,
,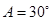
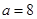 ,
,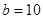 ,
,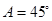
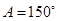
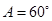
 ,
,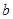 ,
, 分别是△ABC的角
分别是△ABC的角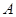 ,
,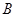 ,
, 的对边,
的对边, ,
,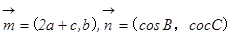 且
且 .
. ,
, ,求
,求 中,设角
中,设角 所对边分别为
所对边分别为 ,若
,若 ,则角
,则角 .
. 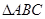 中,若
中,若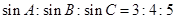 ,则
,则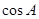 的值为
的值为