题目内容
已知函数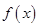 的自变量的取值区间为A,若其值域区间也为A,则称A为
的自变量的取值区间为A,若其值域区间也为A,则称A为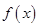 的保值区间.
的保值区间.
(Ⅰ)求函数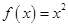 形如
形如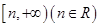 的保值区间;
的保值区间;
(Ⅱ)函数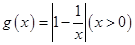 是否存在形如
是否存在形如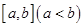 的保值区间?若存在,求出实数
的保值区间?若存在,求出实数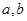 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(Ⅰ)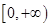 或
或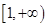 .(Ⅱ)不存在
.(Ⅱ)不存在
解析试题分析:(Ⅰ)因为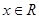 时
时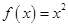 值域为
值域为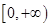 。所以要使
。所以要使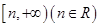 为保值区间,则
为保值区间,则 。根据保值区间的定义可得
。根据保值区间的定义可得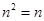 ,解方程即可得
,解方程即可得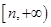 。(Ⅱ)将
。(Ⅱ)将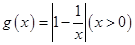 去绝对值改写为分段函数,讨论其单调性。同时讨论
去绝对值改写为分段函数,讨论其单调性。同时讨论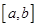 与单调区间的关系。根据保值区间的定义列方程计算。
与单调区间的关系。根据保值区间的定义列方程计算。
试题解析:解(Ⅰ) ,又
,又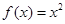 在
在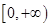 是增函数,
是增函数,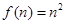 .
. 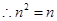 .
. 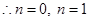 .
. 函数
函数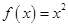 形如
形如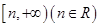 的保值区间有
的保值区间有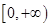 或
或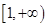 . 2分
. 2分
(Ⅱ)假设存在实数a,b使得函数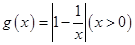 ,有形如
,有形如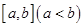 的保值区间,则
的保值区间,则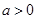 .
.  4分
4分
当实数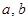
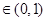 时,
时,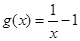 在
在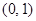 上为减函数,故
上为减函数,故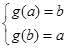 ,
,
即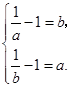
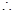
 =b与
=b与 <b矛盾.
<b矛盾.
故此情况不存在满足条件的实数a,b. 5分
(2)当实数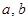
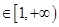 时,
时,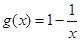 在
在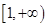 为增函数,故
为增函数,故
即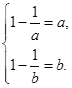 得方程
得方程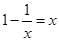 在
在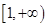 上有两个不等的实根,而
上有两个不等的实根,而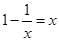 ,
,
即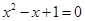 无实根.
无实根.
故此情况不存在满足条件的实数a,b. 6分
(3)当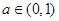 ,
,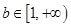 ,
,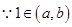 ,而
,而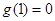 ,
,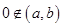 .
.
故此情况不存在满足条件的实数a,b. 7分
综上所述,不存在实数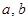 使得函数
使得函数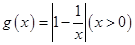 ,有形如
,有形如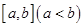 的保值区间. 8分
的保值区间. 8分
考点:对新概念的理解和运用,考查对所学知识的综合运用及分析能力和解决问题的能力。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
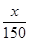 +2是否符合公司要求的奖励函数模型,并说明原因;
+2是否符合公司要求的奖励函数模型,并说明原因;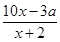 作为奖励函数模型,试确定最小的正整数a的值.
作为奖励函数模型,试确定最小的正整数a的值.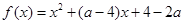 .
. 是偶函数,求实数
是偶函数,求实数 的值;
的值;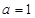 时,求
时,求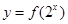 在区间
在区间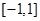 上的值域.
上的值域. 平方米.
平方米.
 表示
表示 和用
和用 R.
R.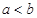 ,比较
,比较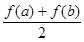 与
与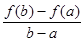 的大小并说明理由。
的大小并说明理由。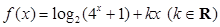 是偶函数。
是偶函数。 的值;
的值;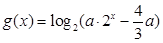 ,其中实数
,其中实数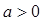 。若函数
。若函数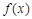 与
与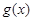 的图象有且只有一个交点,求实数
的图象有且只有一个交点,求实数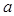 的取值范围。
的取值范围。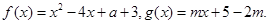
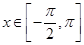 时,若函数
时,若函数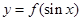 存在零点,求实数
存在零点,求实数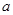 的取值范围并讨论零点个数;
的取值范围并讨论零点个数;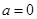 时,若对任意的
时,若对任意的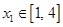 ,总存在
,总存在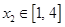 ,使
,使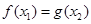 成立,求实数
成立,求实数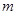 的取值范围.
的取值范围.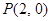 ,点
,点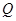 在曲线
在曲线 :
: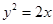 上.
上.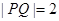 ,求点
,求点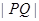 的最小值.
的最小值.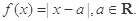
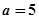 ,解不等式
,解不等式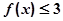 ;
;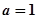 时,若
时,若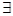
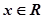 ,使得不等式
,使得不等式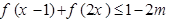 成立,求实数
成立,求实数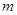 的取值范围.
的取值范围.