题目内容
设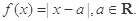
(Ⅰ)当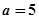 ,解不等式
,解不等式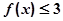 ;
;
(Ⅱ)当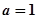 时,若
时,若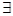
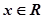 ,使得不等式
,使得不等式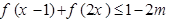 成立,求实数
成立,求实数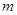 的取值范围.
的取值范围.
(1)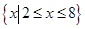 ;(2)
;(2)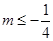 .
.
解析试题分析:本题考查绝对值不等式的解法和不等式恒成立问题,考查转化思想和分类讨论思想.第一问,先将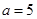 代入,解绝对值不等式;第二问,先将
代入,解绝对值不等式;第二问,先将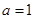 代入,得出
代入,得出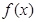 解析式,将已知条件转化为求最小值问题,将
解析式,将已知条件转化为求最小值问题,将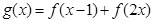 去绝对值转化为分段函数,通过函数图像,求出最小值,所以
去绝对值转化为分段函数,通过函数图像,求出最小值,所以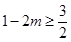 ,再解不等式即可.
,再解不等式即可.
试题解析:(I)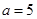 时原不等式等价于
时原不等式等价于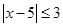 即
即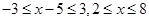 ,
,
所以解集为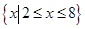 . 5分
. 5分
(II)当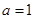 时,
时,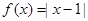 ,令
,令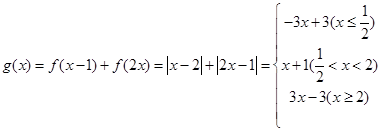 ,
,
由图像知:当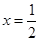 时,
时,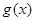 取得最小值
取得最小值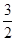 ,由题意知:
,由题意知: ,
,
所以实数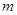 的取值范围为
的取值范围为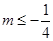 . 10分
. 10分
考点:1.解绝对值不等式;2.分段函数图像;3.存在性问题的解法.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
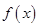 的自变量的取值区间为A,若其值域区间也为A,则称A为
的自变量的取值区间为A,若其值域区间也为A,则称A为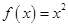 形如
形如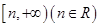 的保值区间;
的保值区间;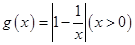 是否存在形如
是否存在形如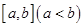 的保值区间?若存在,求出实数
的保值区间?若存在,求出实数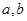 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.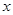 万件(假设该厂生产的产品全部销售),与年促销费用
万件(假设该厂生产的产品全部销售),与年促销费用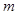 万元
万元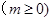 近似满足
近似满足 ,如果不促销,该产品的年销售量只能是1万件.已知2013年生产该产品的固定投入10万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格规定为每件产品成本的1.5倍.(产品成本包括固定投入和再投入两部分资金).
,如果不促销,该产品的年销售量只能是1万件.已知2013年生产该产品的固定投入10万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格规定为每件产品成本的1.5倍.(产品成本包括固定投入和再投入两部分资金).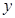 万元表示为年促销费用
万元表示为年促销费用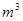 ,如果每年平均增长5﹪,经过
,如果每年平均增长5﹪,经过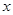 年,树林中有木材
年,树林中有木材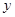
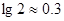 ,
,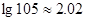 )
)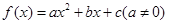 的图像顶点为
的图像顶点为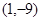 ,且图像在
,且图像在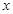 轴截得的线段长为6.
轴截得的线段长为6.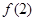 ;
; 在区间
在区间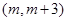 上单调,求
上单调,求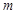 的范围.
的范围. 元,
元,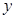 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格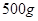 ,按每年
,按每年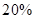 衰减.
衰减.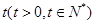 年后,这种放射性元素的质量
年后,这种放射性元素的质量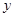 与
与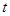 的函数关系式;
的函数关系式;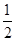 时所经历的时间).(
时所经历的时间).(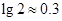 )
) 在
在 上单调递减且满足
上单调递减且满足 .
. 的取值范围.
的取值范围. ,求
,求 在
在 构成的:对于定义域内任意两个不相等的实数
构成的:对于定义域内任意两个不相等的实数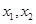 ,都有
,都有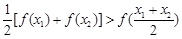 .
.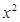 及
及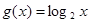 是否在集合A中,并说明理由;
是否在集合A中,并说明理由; ,试写出一个满足以上条件的函数
,试写出一个满足以上条件的函数