题目内容
2. 如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°
如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°(I)求证:PB⊥AD;
(II)若PB=$\sqrt{6}$,求二面角A-PD-C的余弦值.
分析 (Ⅰ)证明:取AD的中点E,连接PE,BE,BD.证明AD⊥平面PBE,然后证明PB⊥AD;
(Ⅱ)以点E为坐标原点,分别以EA,EB,EP所在直线为x,y,z轴,建立如图所示空间直角坐标系,求出平面APD的一个法向量为$\overrightarrow{m}$=(0,1,0),平面PDC的一个法向量为$\overrightarrow{n}$,利用向量的数量积求解二面角A-PD-C的余弦值.
解答 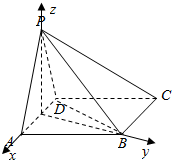 (Ⅰ)证明:取AD的中点E,连接PE,BE,BD.
(Ⅰ)证明:取AD的中点E,连接PE,BE,BD.
∵PA=PD=DA,四边形ABCD为菱形,且∠BAD=60°,
∴△PAD和△ABD为两个全等的等边三角形,
则PE⊥AD,BE⊥AD,∴AD⊥平面PBE,…(3分)
又PB?平面PBE,∴PB⊥AD;…(5分)
(Ⅱ)解:在△PBE中,由已知得,PE=BE=$\sqrt{3}$,PB=$\sqrt{6}$,则PB2=PE2+BE2,
∴∠PEB=90°,即PE⊥BE,又PE⊥AD,∴PE⊥平面ABCD;
以点E为坐标原点,分别以EA,EB,EP所在直线为x,y,z轴,建立如图所示空间直角坐标系,
则E(0,0,0),C(-2,$\sqrt{3}$,0),D(-1,0,0),P(0,0,$\sqrt{3}$),
则$\overrightarrow{PD}$=(1,0,$\sqrt{3}$),$\overrightarrow{DC}$=(-1,$\sqrt{3}$,0),
由题意可设平面APD的一个法向量为$\overrightarrow{m}$=(0,1,0);…(7分)
设平面PDC的一个法向量为$\overrightarrow{n}$=(x,y,z),
由 得:$\left\{\begin{array}{l}{x+\sqrt{3}z=0}\\{-x+\sqrt{3}y=0}\end{array}\right.$,
令y=1,则x=$\sqrt{3}$,z=-1,∴$\overrightarrow{n}$=($\sqrt{3}$,1,-1);
则$\overrightarrow{m}$•$\overrightarrow{n}$=1,∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$,…(11分)
由题意知二面角A-PD-C的平面角为钝角,
所以,二面角A-PD-C的余弦值为-$\frac{\sqrt{5}}{5}$…(12分)
点评 本题考查直线与平面垂直,二面角的平面角的求法,考查逻辑推理以及计算能力.

 如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )
如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )| A. | 1:1 | B. | $\sqrt{2}$:1 | C. | $\sqrt{2}$:2 | D. | 1:2 |
| A. | (-∞,-1] | B. | (-∞,0] | C. | [0,+∞) | D. | [1,+∞) |
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{5}$ | D. | $\sqrt{5}$ |
| A. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{12}$=1 | B. | $\frac{{y}^{2}}{3}$-$\frac{{x}^{2}}{12}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{3}$=1 |
