题目内容
12. 如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )
如图所示,已知矩形ABCD与ABEF全等,D-AB-E为直二面角,M为AB的中点,FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,则AB与BC的长度之比为( )| A. | 1:1 | B. | $\sqrt{2}$:1 | C. | $\sqrt{2}$:2 | D. | 1:2 |
分析 以A为原点,AF为x轴,AB为y轴,AD为z轴,建立空间直角坐标系,设AB=2a,BC=2b,利用向量法能求出AB与BC的长度之比.
解答 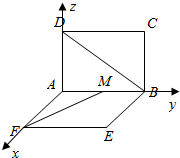 解:以A为原点,AF为x轴,AB为y轴,AD为z轴,建立空间直角坐标系,
解:以A为原点,AF为x轴,AB为y轴,AD为z轴,建立空间直角坐标系,
设AB=2a,BC=2b,
则F(2b,0,0),M(0,a,0),B(0,2a,0),D(0,0,2b),
$\overrightarrow{FM}$=(-2b,a,0),$\overrightarrow{BD}$=(0,-2a,2b),
∵FM与BD所成角为θ,且cosθ=$\frac{\sqrt{3}}{9}$,
∴|cos<$\overrightarrow{FM},\overrightarrow{BD}$>|=|$\frac{\overrightarrow{FM}•\overrightarrow{BD}}{|\overrightarrow{FM}|•|\overrightarrow{BD}|}$|=|$\frac{-2{a}^{2}}{\sqrt{{a}^{2}+4{b}^{2}}•\sqrt{4{a}^{2}+4{b}^{2}}}$|=$\frac{\sqrt{3}}{9}$,
整理,得5a2b2+4b4-26a4=0,
∴$4×(\frac{{b}^{2}}{{a}^{2}})^{2}$+5×$\frac{{a}^{2}}{{b}^{2}}$-26=0,解得$\frac{{a}^{2}}{{b}^{2}}$=2,或$\frac{{a}^{2}}{{b}^{2}}$=-$\frac{13}{4}$(舍),
∴$a=\sqrt{2}b$,
∴AB与BC的长度之比为:2a:2b=a:b=$\sqrt{2}$:1.
故选:B.
点评 本题考查两线段长的比值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

 启东小题作业本系列答案
启东小题作业本系列答案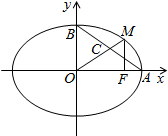 (Ⅰ)求过点($\sqrt{3},2\sqrt{2}$)且与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有相同渐近线的双曲线的标准方程.
(Ⅰ)求过点($\sqrt{3},2\sqrt{2}$)且与双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$有相同渐近线的双曲线的标准方程.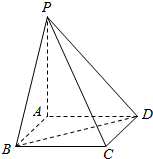 已知PA垂直于矩形ABCD所在平面,PA=3,AB=1,BC=$\sqrt{3}$.
已知PA垂直于矩形ABCD所在平面,PA=3,AB=1,BC=$\sqrt{3}$.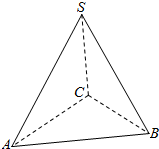
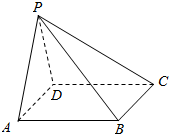 如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°
如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°