题目内容
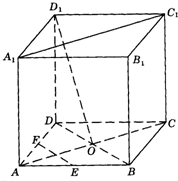 如图,在棱长为a的正方体ABCD-A1B1C1D1中,O是AC、BD的交点,E,F分别是AB与AD的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,O是AC、BD的交点,E,F分别是AB与AD的中点.(1)求证:直线OD1与直线A1C1垂直;
(2)求异面直线EF与A1C1所成角的大小;
(3)求二面角B-AC-D1的大小.
分析:(1)根据A1C1∥AC,可知AC与OD1所成的角就是所求的角,然后根据AC⊥平面D1DO,从而直线OD1与直线A1C1垂直;
(2)根据A1C1∥AC,可知AC与EF所成的角就是所求的角,又E,F分别是AB,AD的中点,从而求出EF与A1C1所成的角;
(3)根据二面角平面角的定义可知∠D1OB是二面角B-AC-D1的平面角,然后在三角形D1OB中用余弦定理求出此角的余弦值即可求出此角.
(2)根据A1C1∥AC,可知AC与EF所成的角就是所求的角,又E,F分别是AB,AD的中点,从而求出EF与A1C1所成的角;
(3)根据二面角平面角的定义可知∠D1OB是二面角B-AC-D1的平面角,然后在三角形D1OB中用余弦定理求出此角的余弦值即可求出此角.
解答:解:(1)∵A1C1∥AC,∴AC与OD1所成的角就是所求的角; …(1分)
∵AC⊥BD,AC⊥DD1,∴AC⊥平面D1DO…(3分)
∴AC⊥OD1,即OD1与AC所成的角为90°…(5分)
∴直线OD1与直线A1C1垂直;
(2)∵A1C1∥AC,∴AC与EF所成的角就是所求的角; …(6分)
又E,F分别是AB,AD的中点,∴AC⊥EF…(8分)
则EF与A1C1所成的角为90°…(10分)
(3)∵BO⊥AC,D1O⊥AC,∴∠D1OB是二面角B-AC-D1的平面角…(12分)
在△D1OB中,BO=
a,OD1=
a,BD1=
a,
由余弦定理得:cos∠D1OB=
=-
…(15分)
因此,所求二面角B-AC-D1的大小为π-arccos
…(16分)
∵AC⊥BD,AC⊥DD1,∴AC⊥平面D1DO…(3分)
∴AC⊥OD1,即OD1与AC所成的角为90°…(5分)
∴直线OD1与直线A1C1垂直;
(2)∵A1C1∥AC,∴AC与EF所成的角就是所求的角; …(6分)
又E,F分别是AB,AD的中点,∴AC⊥EF…(8分)
则EF与A1C1所成的角为90°…(10分)
(3)∵BO⊥AC,D1O⊥AC,∴∠D1OB是二面角B-AC-D1的平面角…(12分)
在△D1OB中,BO=
| ||
| 2 |
|
| 3 |
由余弦定理得:cos∠D1OB=
| ||||||||
2×
|
| ||
| 3 |
因此,所求二面角B-AC-D1的大小为π-arccos
| ||
| 3 |
点评:本题主要考查了异面直线所成角的度量以及线面垂直的判定,同时考查了二面角平面角的度量,属于中档题.

练习册系列答案
相关题目
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( ) ,当
,当 取什么位置时,三棱柱的体积最大?
取什么位置时,三棱柱的体积最大?





