题目内容
甲、乙两容器中分别盛有两种浓度的某种溶液 ,从甲容器中取出
,从甲容器中取出 溶液,将其倒入乙容器中搅匀,再从乙容器中取出
溶液,将其倒入乙容器中搅匀,再从乙容器中取出 溶液,将其倒入甲容器中搅匀,这称为是一次调和,已知第一次调和后,甲、乙两种溶液的浓度分别记为:
溶液,将其倒入甲容器中搅匀,这称为是一次调和,已知第一次调和后,甲、乙两种溶液的浓度分别记为: ,
, ,第
,第 次调和后的甲、乙两种溶液的浓度分别记为:
次调和后的甲、乙两种溶液的浓度分别记为: 、
、 .
.
(1)请用 、
、 分别表示
分别表示 和
和 ;
;
(2)问经过多少次调和后,甲乙两容器中溶液的浓度之差小于 .
.
 ,从甲容器中取出
,从甲容器中取出 溶液,将其倒入乙容器中搅匀,再从乙容器中取出
溶液,将其倒入乙容器中搅匀,再从乙容器中取出 溶液,将其倒入甲容器中搅匀,这称为是一次调和,已知第一次调和后,甲、乙两种溶液的浓度分别记为:
溶液,将其倒入甲容器中搅匀,这称为是一次调和,已知第一次调和后,甲、乙两种溶液的浓度分别记为: ,
, ,第
,第 次调和后的甲、乙两种溶液的浓度分别记为:
次调和后的甲、乙两种溶液的浓度分别记为: 、
、 .
.(1)请用
 、
、 分别表示
分别表示 和
和 ;
;(2)问经过多少次调和后,甲乙两容器中溶液的浓度之差小于
 .
.(1)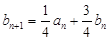 ,
,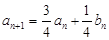 ;(2)
;(2)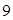 .
.
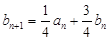 ,
,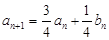 ;(2)
;(2)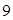 .
.试题分析:(1)根据题中条件归纳出第
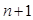 次调和时乙容器中溶质的量
次调和时乙容器中溶质的量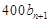 等于从甲容器中取出的溶质的量
等于从甲容器中取出的溶质的量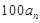 以及从乙容器中本身的溶质的量
以及从乙容器中本身的溶质的量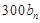 之和,从而得到
之和,从而得到 与
与 和
和 之间的关系,利用同样的方法得到
之间的关系,利用同样的方法得到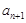 与
与 与
与 ,从而实现利用
,从而实现利用 和
和 来表示
来表示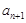 ;(2)利用(1)中的表达式并结合定义得到数列
;(2)利用(1)中的表达式并结合定义得到数列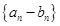 为等比数列,求出该数列的首项与公比,确定数列
为等比数列,求出该数列的首项与公比,确定数列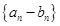 的通项公式,然后解不等式
的通项公式,然后解不等式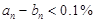 ,求出相应的
,求出相应的 即可.
即可.(1)由题意可设在第一次调和后的浓度为
 ,
, ,
,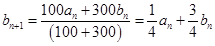 ;
;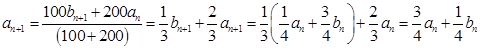
(2)由于题目中的问题是针对浓度之差,所以,我们不妨直接考虑数列
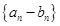 .
.由(1)可得:
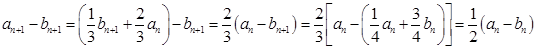 ,
,所以,数列
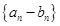 是以
是以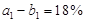 为首项,以
为首项,以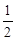 为公比的等比数列.
为公比的等比数列.所以,
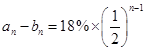 ,
,由题,令
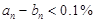 ,得
,得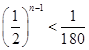 .所以,
.所以, ,
,由
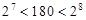 得
得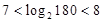 ,所以,
,所以,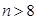 .
. 即第
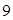 次调和后两溶液的浓度之差小于
次调和后两溶液的浓度之差小于 .
.
练习册系列答案
相关题目
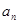 }中,
}中,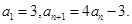
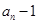 }是等比数列,并求出数列{
}是等比数列,并求出数列{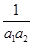 +
+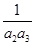 +…+
+…+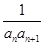 的结果可化为( )
的结果可化为( )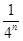
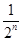
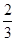 (1-
(1- 的前n项和为
的前n项和为 ,已知
,已知 成等差数列,则数列
成等差数列,则数列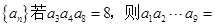 ________.
________. ,则2a7+a11的最小值为( )
,则2a7+a11的最小值为( ) 的前
的前 项积为
项积为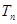 ,若
,若 ,则
,则 =__________.
=__________.